
【题目】设等差数列{an}满足3a8=5a15 , 且 ![]() ,Sn为其前n项和,则数列{Sn}的最大项为( )
,Sn为其前n项和,则数列{Sn}的最大项为( )
A.![]()
B.S24
C.S25
D.S26
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱台DEF﹣ABC中,AB=2DE,G,H分别为AC,BC的中点.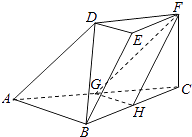
(Ⅰ)求证:BD∥平面FGH;
(Ⅱ)若CF⊥平面ABC,AB⊥BC,CF=DE,∠BAC=45°,求平面FGH与平面ACFD所成的角(锐角)的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx
(1)当a=1时,求f(x)的单调区间;
(2)若函数f(x)在(0, ![]() )上无零点,求a最小值.
)上无零点,求a最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若a∈R,则“ ![]() <1”是“a>1”的必要不充分条件
<1”是“a>1”的必要不充分条件
B.“p∧q为真命题”是“p∨q为真命题”的必要不充分条件
C.若命题p:“x∈R,sinx+cosx≤ ![]() ”,则¬p是真命题
”,则¬p是真命题
D.命题“x0∈R,使得x02+2x0+3<0”的否定是“x∈R,x2+2x+3>0”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ﹣alnx.
﹣alnx.
(Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求函数y=f(x)的单调区间和极值;
(Ⅲ)若函数f(x)在区间(1,e2]内恰有两个零点,试求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=2ln(x﹣2)﹣a(x﹣2)2
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若函数f(x)有两个相异零点x1 , x2 , 求证x1x2+4>2(x1+x2)+e(其中e为自然对数的底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=(x+1)ex则对任意的m∈R,函数F(x)=f(f(x))﹣m的零点个数至多有( )
A.3个
B.4个
C.6个
D.9个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线l的参数方程为 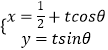 ,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2α﹣2cosα=0.
,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2α﹣2cosα=0.
(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A,B两点,当θ变化时,求|AB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:今有刍童,下广三丈,袤四丈,上袤二丈,无广,高一丈,问:积几何?其意思是说:“今有底面为矩形的屋脊状楔体,下底面宽3丈,长4丈;上棱长2丈,高一丈.问它的体积是多少?”已知一丈为10尺,现将该楔体的三视图给出如右图所示,其中网格纸上小正方形的边长为1,则该楔体的体积为( )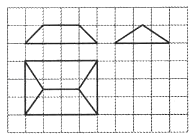
A.5000立方尺
B.5500立方尺
C.6000立方尺
D.6500立方尺
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com