
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:今有刍童,下广三丈,袤四丈,上袤二丈,无广,高一丈,问:积几何?其意思是说:“今有底面为矩形的屋脊状楔体,下底面宽3丈,长4丈;上棱长2丈,高一丈.问它的体积是多少?”已知一丈为10尺,现将该楔体的三视图给出如右图所示,其中网格纸上小正方形的边长为1,则该楔体的体积为( )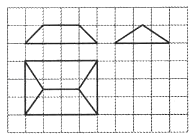
A.5000立方尺
B.5500立方尺
C.6000立方尺
D.6500立方尺
科目:高中数学 来源: 题型:
【题目】命题p:数列{an}的前n项和Sn=an2+bn+c(a≠0);命题q:数列{an}是等差数列.则p是q的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络营销和电子商务的兴起,人们的购物方式更具多样化,某调查机构随机抽取10名购物者进行采访,5名男性购物者中有3名倾向于选择网购,2名倾向于选择实体店,5名女性购物者中有2名倾向于选择网购,3名倾向于选择实体店.
(1)若从10名购物者中随机抽取2名,其中男、女各一名,求至少1名倾向于选择实体店的概率;
(2)若从这10名购物者中随机抽取3名,设X表示抽到倾向于选择网购的男性购物者的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面为矩形的四棱椎P﹣ABCD中,PB⊥AB.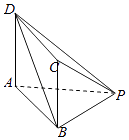
(1)证明:平面PBC⊥平面PCD;
(2)若异面直线PC与BD所成角为60°,PB=AB,PB⊥BC,求二面角B﹣PD﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,首项 ![]() ,前n项和为Sn , 且
,前n项和为Sn , 且 ![]()
(1)求数列{an}的通项
(2)如果bn=3(n+1)×2nan , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=m(x-2m)(x+m+3),g(x)=2x-2.若同时满足条件:
①x∈R,f(x)<0或g(x)<0;
②x∈(-∞,-4),f(x)g(x)<0,则m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B是两个非空集合,定义运算A×B={x|x∈A∪B且xA∩B}.已知A={x|y= ![]() },B={y|y=2x , x>0},则A×B=( )
},B={y|y=2x , x>0},则A×B=( )
A.[0,1]∪(2,+∞)
B.[0,1)∪[2,+∞)
C.[0,1]
D.[0,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确命题的个数是( ) ①对于命题p:x∈R,使得x2+x+1<0,则¬p:x∈R,均有x2+x+1>0;
②命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题;
③回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为 ![]() =1.23x+0.08;
=1.23x+0.08;
④m=3是直线(m+3)x+my﹣2=0与直线mx﹣6y+5=0互相垂直的充要条件.
A.1
B.3
C.2
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com