
【题目】设A,B是两个非空集合,定义运算A×B={x|x∈A∪B且xA∩B}.已知A={x|y= ![]() },B={y|y=2x , x>0},则A×B=( )
},B={y|y=2x , x>0},则A×B=( )
A.[0,1]∪(2,+∞)
B.[0,1)∪[2,+∞)
C.[0,1]
D.[0,2]
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线l的参数方程为 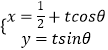 ,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2α﹣2cosα=0.
,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2α﹣2cosα=0.
(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A,B两点,当θ变化时,求|AB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:今有刍童,下广三丈,袤四丈,上袤二丈,无广,高一丈,问:积几何?其意思是说:“今有底面为矩形的屋脊状楔体,下底面宽3丈,长4丈;上棱长2丈,高一丈.问它的体积是多少?”已知一丈为10尺,现将该楔体的三视图给出如右图所示,其中网格纸上小正方形的边长为1,则该楔体的体积为( )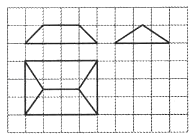
A.5000立方尺
B.5500立方尺
C.6000立方尺
D.6500立方尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线 ![]() 平面
平面 ![]() ,垂足为
,垂足为 ![]() ,正四面体(所有棱长都相等的三棱锥)
,正四面体(所有棱长都相等的三棱锥) ![]() 的棱长为2,
的棱长为2, ![]() 在平面
在平面 ![]() 内,
内, ![]() 是直线
是直线 ![]() 上的动点,当
上的动点,当 ![]() 到
到 ![]() 的距离为最大时,正四面体在平面
的距离为最大时,正四面体在平面 ![]() 上的射影面积为 .
上的射影面积为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月,预测上市初期和后期会因供不应不足使价格呈持续上涨态势,而中期又将出现供大于求使价格连续下跌.现有三种价格模拟函数:
① ![]() ;②
;② ![]() ;③
;③ ![]() .(以上三式中、
.(以上三式中、 ![]() 均为常数,且
均为常数,且 ![]() )
)
(1)为准确研究其价格走势,应选哪种价格模拟函数(不必说明理由)
(2)若 ![]() ,
, ![]() ,求出所选函数
,求出所选函数 ![]() 的解析式(注:函数定义域是
的解析式(注:函数定义域是 ![]() .其中
.其中 ![]() 表示8月1日,
表示8月1日, ![]() 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);
(3)在(2)的条件下研究下面课题:为保证养殖户的经济效益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该海鲜将在哪几个月份内价格下跌.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com