
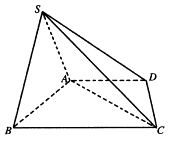
【题目】如图,在四棱锥 ![]() 中,底面梯形
中,底面梯形 ![]() 中,
中, ![]() ,平面
,平面 ![]() 平面
平面 ![]() ,
, ![]() 是等边三角形,已知
是等边三角形,已知 ![]() ,
, ![]() .
.
(1)求证:平面 ![]() 平面
平面 ![]() ;
;
(2)求二面角 ![]() 的余弦值.
的余弦值.
【答案】
(1)证明:在 ![]() 中,由于
中,由于 ![]() ,
,
∴ ![]() ,故
,故 ![]() .
.
又 ![]() ,
,![]() ,∴
,∴ ![]() 平面
平面 ![]() ,
,
又 ![]() ,故平面
,故平面 ![]() 平面
平面 ![]() .
.
(2)如图建立 ![]() 空间直角坐标系,
空间直角坐标系,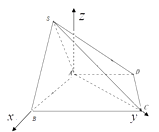
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
设平面 ![]() 的法向量
的法向量 ![]() ,
,
由 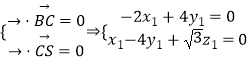
令 ![]() , ∴
, ∴ ![]() .
.
设平面 ![]() 的法向量
的法向量 ![]() ,
,
由 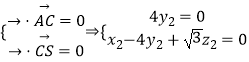 ,令
,令 ![]() ,∴
,∴ ![]() .
.![]() ,∴二面角
,∴二面角 ![]() 的余弦值为
的余弦值为 ![]()
【解析】本题主要考查线面、面面垂直的证明以及利用空间向量求解二面角的大小的问题。(1)把证明面面垂直的问题转化为证明线面垂直,再把线面垂直问题转化为线线垂直问题,利用判定定理进行证明。(2)建立空间直角坐标系,找到坐标,利用二面角公式即可求解。
【考点精析】认真审题,首先需要了解平面与平面垂直的判定(一个平面过另一个平面的垂线,则这两个平面垂直).


科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 的离心率为
的离心率为 ![]() ,F1 , F2分别是它的左、右焦点,且存在直线l,使F1 , F2关于l的对称点恰好为圆C:x2+y2﹣4mx﹣2my+5m2﹣4=0(m∈R,m≠0)的一条直径的两个端点.
,F1 , F2分别是它的左、右焦点,且存在直线l,使F1 , F2关于l的对称点恰好为圆C:x2+y2﹣4mx﹣2my+5m2﹣4=0(m∈R,m≠0)的一条直径的两个端点.
(1)求椭圆E的方程;
(2)设直线l与抛物线y2=2px(p>0)相交于A,B两点,射线F1A,F1B与椭圆E分别相交于点M,N,试探究:是否存在数集D,当且仅当p∈D时,总存在m,使点F1在以线段MN为直径的圆内?若存在,求出数集D;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络营销和电子商务的兴起,人们的购物方式更具多样化,某调查机构随机抽取10名购物者进行采访,5名男性购物者中有3名倾向于选择网购,2名倾向于选择实体店,5名女性购物者中有2名倾向于选择网购,3名倾向于选择实体店.
(1)若从10名购物者中随机抽取2名,其中男、女各一名,求至少1名倾向于选择实体店的概率;
(2)若从这10名购物者中随机抽取3名,设X表示抽到倾向于选择网购的男性购物者的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,首项 ![]() ,前n项和为Sn , 且
,前n项和为Sn , 且 ![]()
(1)求数列{an}的通项
(2)如果bn=3(n+1)×2nan , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=m(x-2m)(x+m+3),g(x)=2x-2.若同时满足条件:
①x∈R,f(x)<0或g(x)<0;
②x∈(-∞,-4),f(x)g(x)<0,则m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B是两个非空集合,定义运算A×B={x|x∈A∪B且xA∩B}.已知A={x|y= ![]() },B={y|y=2x , x>0},则A×B=( )
},B={y|y=2x , x>0},则A×B=( )
A.[0,1]∪(2,+∞)
B.[0,1)∪[2,+∞)
C.[0,1]
D.[0,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆 ![]() 的离心率为
的离心率为 ![]() ,其左焦点到点
,其左焦点到点 ![]() 的距离为
的距离为 ![]() .不过原点
.不过原点 ![]() 的直线
的直线 ![]() 与
与 ![]() 相交于
相交于 ![]() 两点,且线段
两点,且线段 ![]() 被直线
被直线 ![]() 平分.
平分.
(1)求椭圆 ![]() 的方程;
的方程;
(2)求 ![]() 的面积取最大值时直线
的面积取最大值时直线 ![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com