
【题目】已知椭圆E: ![]() 的离心率为
的离心率为 ![]() ,F1 , F2分别是它的左、右焦点,且存在直线l,使F1 , F2关于l的对称点恰好为圆C:x2+y2﹣4mx﹣2my+5m2﹣4=0(m∈R,m≠0)的一条直径的两个端点.
,F1 , F2分别是它的左、右焦点,且存在直线l,使F1 , F2关于l的对称点恰好为圆C:x2+y2﹣4mx﹣2my+5m2﹣4=0(m∈R,m≠0)的一条直径的两个端点.
(1)求椭圆E的方程;
(2)设直线l与抛物线y2=2px(p>0)相交于A,B两点,射线F1A,F1B与椭圆E分别相交于点M,N,试探究:是否存在数集D,当且仅当p∈D时,总存在m,使点F1在以线段MN为直径的圆内?若存在,求出数集D;若不存在,请说明理由.
【答案】
(1)解:将圆C的方程配方的:(x﹣2m)2+(y﹣m)2=4,则圆心C(2m,m),半径为2,
由椭圆的焦距为2c=d=4,c=2,
由e= ![]() =
= ![]() ,则a=3,
,则a=3,
b2=a2﹣c2=5,故椭圆的方程为 ![]() ;
;
(2)由F1,F2关于l的对称点恰好是圆C的一条直径的两个端点,则直线l是线段OC的垂直平分线,
故l方程为y=﹣2x+ ![]() ,
,
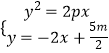 ,整理得2y2+2py﹣5pm=0,
,整理得2y2+2py﹣5pm=0,
则△=(2p)2+4×2×5p>0,则p+10m>0,
设A(x1,y1),B(x1,y1),则y1+y2=﹣p,y1y1=﹣ ![]() ,
,
由F1的坐标为(﹣2,0),则 ![]() =(x1+2,y1),
=(x1+2,y1), ![]() =(x2+2,y2),
=(x2+2,y2),
由 ![]() 与
与 ![]() 同向,
同向, ![]() 与
与 ![]() 同向,
同向,
则点F1在以线段MN为直径的圆内,则 ![]()
![]() <0,则
<0,则 ![]()
![]() <0,
<0,
则(x1+2)(x2+2)+y1y2<0,即x1x2+2(x1+x2)+4+y1y1<0,则 ![]() +10(2﹣p)m+4(p+4)<0,
+10(2﹣p)m+4(p+4)<0,
当且仅当△=100(2﹣p)2﹣100(p+4)>0,即p>5,
总存在m使得②成立,
当p>5时,由韦达定理可知 ![]() +10(2﹣p)m+4(p+4)=0的两个根为正数,
+10(2﹣p)m+4(p+4)=0的两个根为正数,
故使②成立的m>0,从而满足①,
故存在整数集D=(5,+∞),当且仅当p∈D时,总存在m,使点F1在线段MN为直径的圆内.
【解析】(1)将圆C的一般方程变为标准方程,得到圆心坐标和半径,根据题意不难得到椭圆方程中的a,b,c,(2)由F1,F2关于l的对称点恰好是圆C的一条直径的两个端点,则直线l是线段OC的垂直平分线,可得到直线l的方程,联立抛物线方程,由韦达定理得到y1+y2,y1y1,根据点 F1在以线段MN为直径的圆内,可得到 ![]()
![]() <0,表示出向量进行求解即可.
<0,表示出向量进行求解即可.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】一袋中有红、黄、蓝三种颜色的小球各一个,每次从中取出一个,记下颜色后放回,当三种颜色的球全部取出时停止取球,则恰好取5次球时停止取球的概率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若a∈R,则“ ![]() <1”是“a>1”的必要不充分条件
<1”是“a>1”的必要不充分条件
B.“p∧q为真命题”是“p∨q为真命题”的必要不充分条件
C.若命题p:“x∈R,sinx+cosx≤ ![]() ”,则¬p是真命题
”,则¬p是真命题
D.命题“x0∈R,使得x02+2x0+3<0”的否定是“x∈R,x2+2x+3>0”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=2ln(x﹣2)﹣a(x﹣2)2
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若函数f(x)有两个相异零点x1 , x2 , 求证x1x2+4>2(x1+x2)+e(其中e为自然对数的底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=(x+1)ex则对任意的m∈R,函数F(x)=f(f(x))﹣m的零点个数至多有( )
A.3个
B.4个
C.6个
D.9个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线l的参数方程为 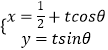 ,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2α﹣2cosα=0.
,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2α﹣2cosα=0.
(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A,B两点,当θ变化时,求|AB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)= ![]() . (a>0且a≠1),函数g(x)=f(x)﹣k.
. (a>0且a≠1),函数g(x)=f(x)﹣k.
①若a= ![]() ,函数g(x)无零点,则实数k的取值范围为;
,函数g(x)无零点,则实数k的取值范围为;
②若f(x)有最小值,则实数a的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com