
【题目】若函数f(x)= ![]() . (a>0且a≠1),函数g(x)=f(x)﹣k.
. (a>0且a≠1),函数g(x)=f(x)﹣k.
①若a= ![]() ,函数g(x)无零点,则实数k的取值范围为;
,函数g(x)无零点,则实数k的取值范围为;
②若f(x)有最小值,则实数a的取值范围是 .
【答案】[﹣1,1),(1,3]
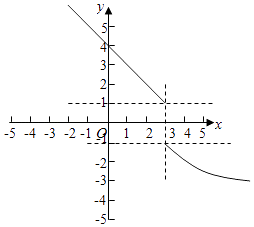
【分析】由数形结合可得①a= ![]() 时,画出函数f(x)的图象,如图所示:若函数g(x)无零点,则y=k和y=f(x)无交点,结合图象,﹣1≤k<1;
时,画出函数f(x)的图象,如图所示:若函数g(x)无零点,则y=k和y=f(x)无交点,结合图象,﹣1≤k<1;
【解析】解:①a= ![]() 时,画出函数f(x)的图象,如图所示:若函数g(x)无零点,则y=k和y=f(x)无交点,结合图象,﹣1≤k<1;
时,画出函数f(x)的图象,如图所示:若函数g(x)无零点,则y=k和y=f(x)无交点,结合图象,﹣1≤k<1;
②若0<a<1,显然f(x)无最小值,故a>1,结合loga3=1,解得:a=3,故a∈(1,3];
所以答案是:[﹣1,1),(1,3].
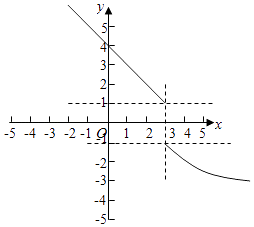
【考点精析】关于本题考查的函数的最值及其几何意义,需要了解利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】某公司对应聘人员进行能力测试,测试成绩总分为150分.下面是30位应聘人员的测试成绩的测试成绩:64,116,82,93,102,82,104,67,93,118,70,95,119,106,83,72,95,106,72,119,122,95,86,74,131,76,88,108,97,123.
(1)求应聘人员的测试成绩的样本平均数 ![]() (保留小数点后两位);
(保留小数点后两位);
(2)根据以上数据完成下面茎叶图:
应聘人员的测试成绩 | |
6 | |
7 | |
8 | |
9 | |
10 | |
11 | |
12 | |
13 | |
(3)由茎叶图可以认为,应聘人员的测试成绩Z服从正态分布N(μ,σ2),其中μ近似为样本平均数 ![]() ,σ2近似为样本方差s2 , 其中s2=18.872 , 利用该正态分布,求P(76.40<Z<114.14).
,σ2近似为样本方差s2 , 其中s2=18.872 , 利用该正态分布,求P(76.40<Z<114.14).
附:若Z~N(μ,σ2),则P(μ﹣σ<Z<μ+σ)=0.6826,
P(μ﹣2σ<Z<μ+2σ)=0.9544.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 的离心率为
的离心率为 ![]() ,F1 , F2分别是它的左、右焦点,且存在直线l,使F1 , F2关于l的对称点恰好为圆C:x2+y2﹣4mx﹣2my+5m2﹣4=0(m∈R,m≠0)的一条直径的两个端点.
,F1 , F2分别是它的左、右焦点,且存在直线l,使F1 , F2关于l的对称点恰好为圆C:x2+y2﹣4mx﹣2my+5m2﹣4=0(m∈R,m≠0)的一条直径的两个端点.
(1)求椭圆E的方程;
(2)设直线l与抛物线y2=2px(p>0)相交于A,B两点,射线F1A,F1B与椭圆E分别相交于点M,N,试探究:是否存在数集D,当且仅当p∈D时,总存在m,使点F1在以线段MN为直径的圆内?若存在,求出数集D;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:数列{an}的前n项和Sn=an2+bn+c(a≠0);命题q:数列{an}是等差数列.则p是q的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,四边形ABCD的各顶点均在椭圆E上,且对角线AC,BD均过坐标原点O,点D(2,1),AC,BD的斜率之积为
,四边形ABCD的各顶点均在椭圆E上,且对角线AC,BD均过坐标原点O,点D(2,1),AC,BD的斜率之积为 ![]() .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过D作直线l平行于AC.若直线l′平行于BD,且与椭圆E交于不同的两点M.N,与直线l交于点P.
⑴证明:直线l与椭圆E有且只有一个公共点;
⑵证明:存在常数λ,使得|PD|2=λ|PM||PN|,并求出λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络营销和电子商务的兴起,人们的购物方式更具多样化,某调查机构随机抽取10名购物者进行采访,5名男性购物者中有3名倾向于选择网购,2名倾向于选择实体店,5名女性购物者中有2名倾向于选择网购,3名倾向于选择实体店.
(1)若从10名购物者中随机抽取2名,其中男、女各一名,求至少1名倾向于选择实体店的概率;
(2)若从这10名购物者中随机抽取3名,设X表示抽到倾向于选择网购的男性购物者的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,首项 ![]() ,前n项和为Sn , 且
,前n项和为Sn , 且 ![]()
(1)求数列{an}的通项
(2)如果bn=3(n+1)×2nan , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆 ![]() 的离心率为
的离心率为 ![]() ,其左焦点到点
,其左焦点到点 ![]() 的距离为
的距离为 ![]() .不过原点
.不过原点 ![]() 的直线
的直线 ![]() 与
与 ![]() 相交于
相交于 ![]() 两点,且线段
两点,且线段 ![]() 被直线
被直线 ![]() 平分.
平分.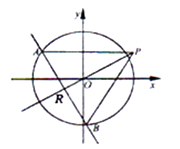
(1)求椭圆 ![]() 的方程;
的方程;
(2)求 ![]() 的面积取最大值时直线
的面积取最大值时直线 ![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com