
【题目】已知命题p:m∈R且m+1≤0;命题q:x∈R,x2+mx+1>0恒成立.若p∧q为假命题,则m的取值范围是 .
【答案】(-∞,-2]∪(-1,+∞)
【解析】先分别求出命题 ![]() 满足的条件(
满足的条件( ![]() 取值的范围)分别为
取值的范围)分别为 ![]() ,再依据题设可推证出命题
,再依据题设可推证出命题 ![]() 中只有一个命题是正确的的结论:然后分类为“
中只有一个命题是正确的的结论:然后分类为“ ![]() 真
真 ![]() 假”或“
假”或“ ![]() 假
假 ![]() 真”建立关于实数
真”建立关于实数 ![]() 的不等式组
的不等式组 ![]() 或
或 ![]() ,通过解不等式组求解:
,通过解不等式组求解:
命题p:m∈R且m+1≤0,解得m ![]() ﹣1.
﹣1.
命题q:x∈R,x2+mx+1>0恒成立
∴△=m2-4<0,解得-2<m<2.
若“p∨q”为真,“p∧q”为假,
则p与q必然一真一假,
∴ ![]() 或
或 ![]() ,
,
解得﹣1<m<2或m ![]() -2.
-2.
∴实数m的取值范围是﹣1<m<2或m ![]() -2.
-2.
由题意分别求出命题P,q为真时m的范围,再根据p∧q为假命题且p∨q为真命题时,命题P,q一真一假求得m的集合.判断复合命题的真假要根据真值表来判定.


科目:高中数学 来源: 题型:
【题目】在数列{an}中,首项 ![]() ,前n项和为Sn , 且
,前n项和为Sn , 且 ![]()
(1)求数列{an}的通项
(2)如果bn=3(n+1)×2nan , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B是两个非空集合,定义运算A×B={x|x∈A∪B且xA∩B}.已知A={x|y= ![]() },B={y|y=2x , x>0},则A×B=( )
},B={y|y=2x , x>0},则A×B=( )
A.[0,1]∪(2,+∞)
B.[0,1)∪[2,+∞)
C.[0,1]
D.[0,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若图,在三棱柱 ![]() 中,平面
中,平面 ![]() 平面
平面 ![]() ,且
,且 ![]() 和
和 ![]() 均为正三角形.
均为正三角形.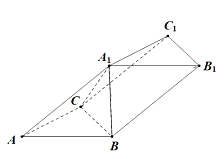
(1)在 ![]() 上找一点
上找一点 ![]() ,使得
,使得 ![]() 平面
平面 ![]() ,并说明理由.
,并说明理由.
(2)若 ![]() 的面积为
的面积为 ![]() ,求四棱锥
,求四棱锥 ![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆 ![]() 的离心率为
的离心率为 ![]() ,其左焦点到点
,其左焦点到点 ![]() 的距离为
的距离为 ![]() .不过原点
.不过原点 ![]() 的直线
的直线 ![]() 与
与 ![]() 相交于
相交于 ![]() 两点,且线段
两点,且线段 ![]() 被直线
被直线 ![]() 平分.
平分.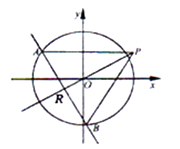
(1)求椭圆 ![]() 的方程;
的方程;
(2)求 ![]() 的面积取最大值时直线
的面积取最大值时直线 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 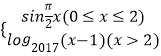 ,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( )
,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( )
A.(4,2018)
B.(4,2020)
C.(3,2020)
D.(2,2020)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com