练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x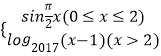）= ，若a，b，c互不相等，且f（a）=f（b）=f（c），则a+b+c的取值范围是（ ）
    A.（4，2018）
    B.（4，2020）
    C.（3，2020）
    D.（2，2020）

    【答案】B
    【解析】解：作出函数的图象如图，直线y=m交函数图象于如图，

    不妨设a＜b＜c，

    由正弦曲线的对称性，可得（a，m）与（b，m）关于直线x=1对称，

    因此a+b=2．

    当直线y=m=1时，由log2017（x﹣1）=1，

    解得x﹣1=2017，即x=2018，

    ∴若满足f（a）=f（b）=f（c），（a、b、c互不相等），

    由a＜b＜c可得2＜c＜2018，

    因此可得4＜a+b+c＜2020，

    即a+b+c∈（4，2020），

    故选：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知命题p：m∈R且m＋1≤0；命题q：x∈R，x2＋mx＋1>0恒成立．若p∧q为假命题，则m的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明，下面是赵爽的弦图及注文，弦图是一个以勾股形之弦为边的正方形，其面积称为弦实，图中包含四个全等的勾股形及一个小正方形，分别涂成红（朱）色及黄色，其面积称为朱实，黄实，利用2×勾×股+（股﹣勾）2=4×朱实+黄实=弦实，化简，得勾2+股2=弦2 ， 设勾股中勾股比为1： ，若向弦图内随机抛掷1000颗图钉（大小忽略不计），则落在黄色图形内的图钉数大约为（ ）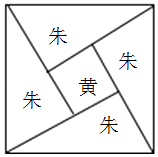
    A.866
    B.500
    C.300
    D.134

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆锥曲线 ( 是参数)和定点 , 、 是圆锥曲线的左、右焦点．
    （1）求经过点 且垂直于直线 的直线 的参数方程；
    （2）以坐标原点为极点， 轴的正半轴为极轴建立极坐标系，求直线 的极坐标方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥 中， 是等边三角形， 是 的中点， ，二面角 的大小为 ．

    （1）求证：平面 平面 ；
    （2）求 与平面 所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知x，y∈R，且 ，则存在θ∈R，使得xcosθ+ysinθ+1=0成立的P（x，y）构成的区域面积为（ ）
    A.4 ﹣
    B.4 ﹣
    C.
    D. +

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在极坐标系下，知圆O：ρ=cosθ+sinθ和直线 ．
    （1）求圆O与直线l的直角坐标方程；
    （2）当θ∈（0，π）时，求圆O和直线l的公共点的极坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆 ： 的离心率为 ，且以两焦点为直径的圆的内接正方形面积为2．
    （1）求椭圆 的标准方程；
    （2）若直线 ： 与椭圆 相交于 ， 两点，在 轴上是否存在点 ，使直线 与 的斜率之和 为定值？若存在，求出点 坐标及该定值，若不存在，试说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

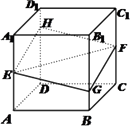
    【题目】如图，正方体 的棱长为1， 分别是棱 的中点，过 的平面与棱 分别交于点 .设 ， ．

    ①四边形 一定是菱形；② 平面 ；③四边形 的面积 在区间 上具有单调性；④四棱锥 的体积为定值.
    以上结论正确的个数是（ ）
    A.4
    B.3
    C.2
    D.1

    查看答案和解析>>

    同步练习册答案