
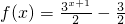 图象上.
图象上.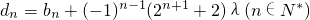 ,若dn+1>dn,n∈N*成立,试证明:
,若dn+1>dn,n∈N*成立,试证明: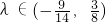 .
.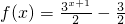 图象上.
图象上. +
+ ;
; ,dn+1>dn,n∈N*成立,
,dn+1>dn,n∈N*成立, =
=
 =-
=-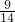
 ;
; =
=
 =
=

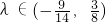 .
.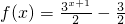 图象上,可求数列{bn}的通项公式;
图象上,可求数列{bn}的通项公式;

科目:高中数学 来源: 题型:单选题

 ,b=7
,b=7 ,b=-7
,b=-7查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 时,若元素x∈A是x∈B的必要条件,求实数a的取值范围.
时,若元素x∈A是x∈B的必要条件,求实数a的取值范围.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x∕106元 | 2 | 4 | 5 | 6 | 8 |
| y∕106元 | 30 | 40 | 60 | 50 | 70 |
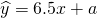 ,则a的值为________.
,则a的值为________.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
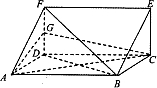 已知三棱柱ADF-BCE中,DF⊥平面ABCD,G是DF的中点.
已知三棱柱ADF-BCE中,DF⊥平面ABCD,G是DF的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com