
已知等比数列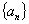 中各项均为正,有
中各项均为正,有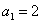 ,
,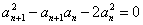 ,
,
等差数列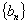 中,
中, ,点
,点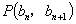 在直线
在直线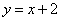 上.
上.
(1)求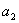 和
和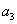 的值;(2)求数列
的值;(2)求数列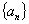 ,
,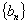 的通项
的通项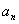 和
和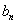 ;
;
(3)设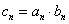 ,求数列
,求数列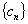 的前n项和
的前n项和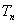 .
.
解:(1)∵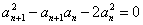
∴ ,又
,又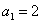
解得 ,
, (舍去)
(舍去)
 ,解得
,解得 ,
, (舍去)
(舍去)
(2)∵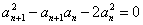
∴ ,
,
∵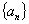 中各项均为正,∴
中各项均为正,∴
又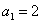 ∴即数列
∴即数列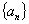 是以2为首项以为2公比的等比数列
是以2为首项以为2公比的等比数列
∴ ……6分
……6分
∵点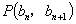 在直线
在直线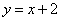 上,∴
上,∴ ,
,
又 ∴数列
∴数列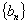 是以1为首项以为2公差的等差数列
是以1为首项以为2公差的等差数列
∴
(3)由(1)得
∴
=1×2+3×22+5×23+····+(2n-1)2n,
∴2Tn=1×22+3×23+····+(2n-3)2n+(2n-1)2n+1
因此:-Tn=1×2+(2×22+2×23+···+2×2n)-(2n-1)2n+1,
即:-Tn=1×2+(23+24+····+2n+1)-(2n-1)2n+1,
∴Tn= (2n-3)2n+1+6


科目:高中数学 来源: 题型:
在某项体育比赛中,七位裁判为一选手打出的分数如下:
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
A.92,2 B.92,2.8
C.93,2 D.93,2.8
查看答案和解析>>
科目:高中数学 来源: 题型:
如图是计算函数y=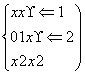 的值的程序框图,则在①、②和③处应分别填入的是( )
的值的程序框图,则在①、②和③处应分别填入的是( )
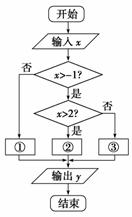
A.y=-x,y=0,y=x2
B.y=-x,y=x2,y=0
C.y=0,y=x2,y=-x
D.y=0,y=-x,y=x2
查看答案和解析>>
科目:高中数学 来源: 题型:
.关于数列有下列四个判断:
①若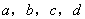 成等比数列,则
成等比数列,则 也成等比数列;②若数列{
也成等比数列;②若数列{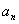 }既是等差数列也是等比数列,则{
}既是等差数列也是等比数列,则{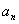 }为常数列;③数列{
}为常数列;③数列{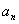 }的前n项和为
}的前n项和为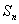 ,且
,且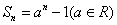 ,则{
,则{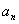 }为等差或等比数列;④数列{
}为等差或等比数列;④数列{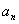 }为等差数列,且公差不为零,则数列{
}为等差数列,且公差不为零,则数列{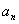 }中不会有
}中不会有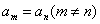 ,其中正确判断的序号是______.(注:把你认为正确判断的序号都填上)
,其中正确判断的序号是______.(注:把你认为正确判断的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
下列说法不正确的是( )
A. 空间中,一组对边平行且相等的四边形是一定是平行四边形;
B.同一平面的两条垂线一定共面;
C. 过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内;
D. 过一条直线有且只有一个平面与已知平面垂直.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com