
已知 在
在 处取得极值,且在点
处取得极值,且在点 处的切线斜率为
处的切线斜率为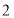 .
.
⑴求 的单调增区间;
的单调增区间;
⑵若关于 的方程
的方程 在区间
在区间 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数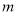 的取值范围.
的取值范围.
(1)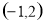 ;(2)
;(2)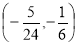
【解析】
试题分析:(1)要求高次函数的单调增区间,只能使用导数法,令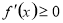 ,解得其增区间.所以得确定其函数解析式.根据导数的几何意义知
,解得其增区间.所以得确定其函数解析式.根据导数的几何意义知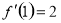 ,根据在
,根据在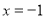 处取得极值,可知
处取得极值,可知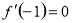 ,解方程组可得
,解方程组可得 解析式.
解析式.
(2)构造新函数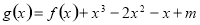 ,根据其在区间
,根据其在区间 上有两个不等的实数根,可知新函数在该区间内与
上有两个不等的实数根,可知新函数在该区间内与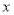 轴有两个不同的交点.根据新函数在该区间内的单调性以及极值建立关系式,解决;
轴有两个不同的交点.根据新函数在该区间内的单调性以及极值建立关系式,解决;
试题解析:⑴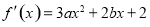 1分;由题意,得
1分;由题意,得
 3分
3分
 ,由
,由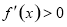 得
得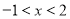 ;
;
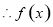 的单调增区间是
的单调增区间是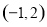 5分
5分
⑵由⑴知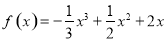 ;
;
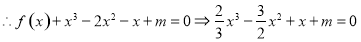 ;
;
令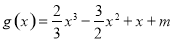 ;
;
则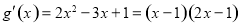 ,由
,由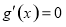 得
得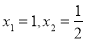 7分;
7分;
当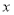 变化时,
变化时,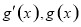 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
| 0 | + |
|
|
| | 极小值 |
|
|
当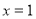 时,
时, 8分
8分
关于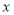 的方程
的方程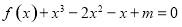 在区间
在区间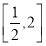 上恰有两个不相等的实数根的充要条件是
上恰有两个不相等的实数根的充要条件是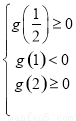 10分,
10分, 12分
12分
考点:函数极值点,利用导数求函数单调区间;利用导数判断函数的变化,从而求未知字母范围.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源:2015届新疆兵团农二师华山中学高二下学期期中理科数学试卷(解析版) 题型:选择题
下列命题错误的
(A)命题“若lnx=0,则x=1”的逆否命题为“若x≠1,则lnx≠0”
(B)“x>2”是“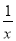 <
<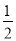 ”的充分不必要条件
”的充分不必要条件
(C)命题p: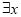 ∈R,使得sinx>1,则
∈R,使得sinx>1,则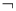 p:
p: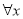 ∈R,均有sinx≤1
∈R,均有sinx≤1
(D)若p∧q为假命题,则p,q均为假命题
查看答案和解析>>
科目:高中数学 来源:2015届新疆兵团农二师华山中学高二下学期期中文科数学试卷(解析版) 题型:选择题
按流程图的程序计算,若开始输入的值为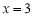 ,则输出的
,则输出的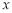 的值是 ( )
的值是 ( )

A.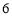 B.
B.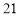 C.
C.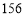 D.
D.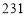
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com