
设m是实数,记M={m|m>1},f(x)=log3(x2-4mx+4m2+m+![]() )
)![]()
(1)证明: 当m∈M时,f(x)对所有实数都有意义;反之,若f(x)对所有实数x都有意义,则m∈M。
(2)当m∈M时,求函数f(x)的最小值。
(3)求证: 对每个m∈M,函数f(x)的最小值都不小于1。
(1) 证明略(2) 当x=m时, f(2m)=log3(m+![]() )为最小值。
)为最小值。
(3)证明略
先将f(x)变形: f(x)=log3[(x-2m)2+m+![]() ],
],
当m∈M时,m>1,∴(x-m)2+m+![]() >0恒成立,
>0恒成立,
故f(x)的定义域为R。
反之,若f(x)对所有实数x都有意义,则只须x2-4mx+4m2+m+![]() >0,令Δ<0,即16m2-4(4m2+m+
>0,令Δ<0,即16m2-4(4m2+m+![]() )<0,解得m>1,故m∈M。
)<0,解得m>1,故m∈M。
(2)解析: 设u=x2-4mx+4m2+m+![]() ,
,
∵y=log3u是增函数,∴当u最小时,f(x)最小。
而u=(x-2m)2+m+![]() ,
,
显然,当x=m时,u取最小值为m+![]() ,
,
此时f(2m)=log3(m+![]() )为最小值。
)为最小值。
(3)证明: 当m∈M时,m+![]() =(m-1)+
=(m-1)+ ![]() +1≥3,
+1≥3,
当且仅当m=2时等号成立。
∴log3(m+![]() )≥log33=1。
)≥log33=1。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 1 | -0.8 |
| 0.1 | -0.3 | -1 |
| 1 | 1 | c |
| a | b | -1 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省达州市万源三中高考数学模拟试卷4(理科)(解析版) 题型:填空题
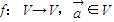 ,记
,记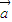 的象为
的象为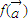 .若映射f:V→V满足:对所有
.若映射f:V→V满足:对所有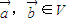 及任意实数λ,μ都有
及任意实数λ,μ都有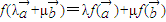 ,则f称为平面M上的线性变换.现有下列命题:
,则f称为平面M上的线性变换.现有下列命题: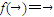
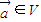 设
设 ,则f是平面M上的线性变换;
,则f是平面M上的线性变换;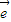 是平面M上的单位向量,对
是平面M上的单位向量,对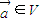 设
设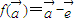 ,则f是平面M上的线性变换;
,则f是平面M上的线性变换;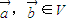 ,若
,若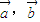 共线,则
共线,则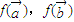 也共线.
也共线.查看答案和解析>>
科目:高中数学 来源:2009年四川省高考数学试卷(理科)(解析版) 题型:解答题
 ,记
,记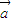 的象为
的象为 .若映射f:V→V满足:对所有
.若映射f:V→V满足:对所有 及任意实数λ,μ都有
及任意实数λ,μ都有 ,则f称为平面M上的线性变换.现有下列命题:
,则f称为平面M上的线性变换.现有下列命题:
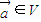 设
设 ,则f是平面M上的线性变换;
,则f是平面M上的线性变换; 是平面M上的单位向量,对
是平面M上的单位向量,对 设
设 ,则f是平面M上的线性变换;
,则f是平面M上的线性变换; ,若
,若 共线,则
共线,则 也共线.
也共线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com