函数f(x)=x2-2x+2在闭区间[t,t+1](t∈R)上的最小值记为g(t).
(1)求g(t)的函数表达式;
(2)作g(t)的简图并写出g(t)的最小值.
分析:(1)由题意可知,f(x)为二次函数,要求其在闭区间[t,t+1](t∈R)上的最小值,主要是分三种情况(区间在对称轴的左边、右边、之间)讨论可得二次函数的最小值即得g(t)的函数表达式;
(2)画出分段函数的简图,由简图可知g(t)的最小值.
解答:解:(1)据题意可知函数为二次函数且开口向上,所以函数有最小值,即当x=-
=
=1,f
min=1
分情况讨论函数在闭区间[t,t+1](t∈R):
①当闭区间[t,t+1](t∈R)?(-∞,1)即t<0时,得:二次函数在x=t+1时取到最小值,
∴g(t)=(t+1)
2-2(t+1)+2=t
2+1;
②当1∈[t,t+1]即0≤t≤1时,得x=1时,二次函数取到最小值∴g(t)=1;
③当闭区间[t,t+1]?(1,+∞)即t>1时,得:x=t时,二次函数取到最小值∴g(t)=t
2-2t+2.
综上
| | g(t)=t2+1 (t<0) | | g(t)=1 (0≤t≤1) | | g(t)=t2-2t+2 (t>1) |
| |
(2)由(1)可知g(t)为分段函数作出图象如下:
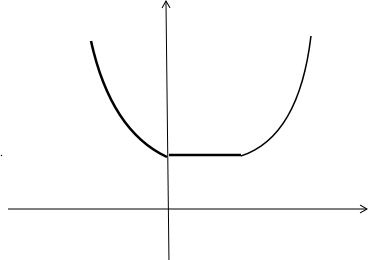
从图象上可知g(t)
min=1.
点评:本题考点是二次函数的图象,考查通过二次函数的图象求二次函数在闭区间上的最值,求解本题主要依据函数的单调性,要根据二次函数的图象判断出所研究区间的单调性,确定最值在那个位置取到,再求出最值,本题中所给的区间是一个不定的区间,故解题时要根据区间与对称轴的位置进行分类讨论,主要是分三种情况(区间在对称轴的左边、右边、之间),解题时注意总结分类讨论思想在求解本题中的作用.




 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案