分析:(1)连AC,A1C1,可先根据线面垂直的判定定理可证BD⊥平面ACC1A1,A1E?平面ACC1A1,根据线面垂直的性质可知BD⊥A1E;
(2)设AC∩BD=O,则O为BD的中点,连A1O,EO,根据二面角平面角的定义可知∠A1OE即为二面角A1-BD-E的平面角,是90°,然后解三角形求出A1E与平面EBD所成角θ的大小即可.
解答: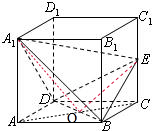
解:(1)证明:连AC,A
1C
1∵正方体AC
1中,AA
1⊥平面ABCD∴AA
1⊥BD
∵正方形ABCD,AC⊥BD且AC∩AA
1=A
∴BD⊥平面ACC
1A
1且E∈CC
1
∴A
1E?平面ACC
1A
1∴BD⊥A
1E
(2)设AC∩BD=O,则O为BD的中点,连A
1O,EO
由(1)得BD⊥平面A
1ACC
1∴BD⊥A
1O,BD⊥EO
∴∠A
1OE即为二面角A
1-BD-E的平面角,
∴∠A
1OE=90°,∴∠OA
1E为A
1E与平面EBD所成角θ,
∵AB=a,E为CC
1中点∴A
1O=
a,EO=
a,A
1E=
a,
sinθ=
=
=
∴θ=arcsin
,此时平面A
1BD⊥平面EBD.
点评:本小题主要考查空间中的线面关系,考查线线垂直、线面垂直的判定,考查空间想象能力、运算能力和推理论证能力.


 解:(1)证明:连AC,A1C1
解:(1)证明:连AC,A1C1

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 16、在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则
16、在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则 如图,在正方体ABCD-A′B′C′D′中,E,F分别是AB′,BC′的中点.
如图,在正方体ABCD-A′B′C′D′中,E,F分别是AB′,BC′的中点.