
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用数学结合,先画出两两垂直的三个平面如图,结合所学知识,证明分析试题选项,即可求得答案.
解答 解:如图: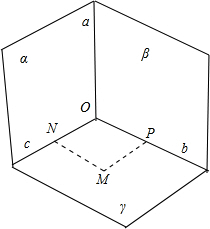
设三个互相垂直的平面分别为α、β、γ,且α∩β=a,β∩γ=b,γ∩α=c,
对于①,因为c与b交于一点,设c∩b=O.由O∈c,且c?α,有O∈α;又由O∈b,且b?β,有O∈β.于是O∈β∩α=a.
所以a,b,c交于一点(即O点),故①正确
对于②,在平面γ内,除点O外,任意取一点M,且点M不在这三个平面中的任何一个平面内,
过点M作MN⊥c,MP⊥b,M、P为垂足,
则有平面和平面垂直的性质可得MN⊥α,MP⊥β,∴a⊥MN,a⊥MP,∴a⊥平面γ.
再由b、c在平面γ内,可得a⊥b,a⊥c.同理可证,c⊥b,c⊥a,从而证得a、b、c互相垂直;
故②正确;
由②知,③也成立,故③正确;
对于④,一个垂直平面α将空间分为两部分,将另一个垂直平面β相交将空间分为4部分,水平平面γ与上述两平面相交,空间即可被此2平面分为8部分,故④正确;
故选:D.
点评 考查了空间图形中线面关系,应紧扣性质和定理去分析.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:选择题
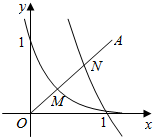 如图,点O为坐标原点,点A(1,1),若函数y=ax(a>0,且a≠1)及logbx(b>0,且b≠1)的图象与线段OA分别交于点M,N,且M,N恰好是线段OA的两个三等分点,则a,b满足( )
如图,点O为坐标原点,点A(1,1),若函数y=ax(a>0,且a≠1)及logbx(b>0,且b≠1)的图象与线段OA分别交于点M,N,且M,N恰好是线段OA的两个三等分点,则a,b满足( )| A. | a<b<1 | B. | b<a<1 | C. | b>a>1 | D. | a>b>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 150° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,m∥β,则α∥β | |
| B. | 若m?α,n?α,l⊥m,l⊥n,则l⊥α | |
| C. | 若m?α,n?α,m,n是异面直线,则n与α相交 | |
| D. | 若m⊥α,m?β,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150° | B. | 120° | C. | 60° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|1≤x<2} | C. | {x|1<x≤2} | D. | {x|1≤x≤2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com