
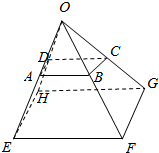
 已知O、A、B、C、D、F、F、G、H为空间9个点(如图),并且$\overrightarrow{OE}$=k$\overrightarrow{OA}$,$\overrightarrow{OF}$=k$\overrightarrow{OB}$,$\overrightarrow{OH}$=k$\overrightarrow{OD}$,$\overrightarrow{AC}$=$\overrightarrow{AD}$+m$\overrightarrow{AB}$,$\overrightarrow{EG}$=$\overrightarrow{EH}$+m$\overrightarrow{EF}$.求证:
已知O、A、B、C、D、F、F、G、H为空间9个点(如图),并且$\overrightarrow{OE}$=k$\overrightarrow{OA}$,$\overrightarrow{OF}$=k$\overrightarrow{OB}$,$\overrightarrow{OH}$=k$\overrightarrow{OD}$,$\overrightarrow{AC}$=$\overrightarrow{AD}$+m$\overrightarrow{AB}$,$\overrightarrow{EG}$=$\overrightarrow{EH}$+m$\overrightarrow{EF}$.求证:分析 (1)由$\overrightarrow{AC}$=$\overrightarrow{AD}$+m$\overrightarrow{AB}$,得$\overrightarrow{AC}$、$\overrightarrow{AD}$、$\overrightarrow{AB}$是共面向量,再由$\overrightarrow{AC}$、$\overrightarrow{AD}$、$\overrightarrow{AB}$有公共点A,能证明A,B,C,D四点共面.
(2)由已知利用向量加法公式能推导出$\overrightarrow{EG}$=$\overrightarrow{EH}+m\overrightarrow{EF}$=k$\overrightarrow{AC}$,由此能证明$\overrightarrow{AC}∥\overrightarrow{EG}$.
(3)由$\overrightarrow{OG}$=$\overrightarrow{EG}-\overrightarrow{EO}$=$k\overrightarrow{AC}-k\overrightarrow{AO}$,能证明$\overrightarrow{OG}=k\overrightarrow{OC}$.
解答 证明:(1)∵$\overrightarrow{AC}$=$\overrightarrow{AD}$+m$\overrightarrow{AB}$,
∴由共面向量基本定理得$\overrightarrow{AC}$、$\overrightarrow{AD}$、$\overrightarrow{AB}$是共面向量,
∵$\overrightarrow{AC}$、$\overrightarrow{AD}$、$\overrightarrow{AB}$有公共点A,
∴A,B,C,D四点共面.
(2)∵$\overrightarrow{EG}$=$\overrightarrow{EH}+m\overrightarrow{EF}$=$\overrightarrow{OH}-\overrightarrow{OE}+m(\overrightarrow{OF}-\overrightarrow{OE})$
=$k(\overrightarrow{AD}-\overrightarrow{OA})+km(\overrightarrow{OB}-\overrightarrow{OA})$
=$k\overrightarrow{AD}+km\overrightarrow{AB}$
=k($\overrightarrow{AD}+m\overrightarrow{AB}$)
=k$\overrightarrow{AC}$,
∴$\overrightarrow{AC}∥\overrightarrow{EG}$.
(3)由(1)知$\overrightarrow{OG}$=$\overrightarrow{EG}-\overrightarrow{EO}$=$k\overrightarrow{AC}-k\overrightarrow{AO}$
=$k(\overrightarrow{AC}-\overrightarrow{AO})$=$k\overrightarrow{OC}$,
∴$\overrightarrow{OG}=k\overrightarrow{OC}$.
点评 判断两个向量$\overrightarrow{a},\overrightarrow{b}$($\overrightarrow{b}≠0$)共线,只需判断$\overrightarrow{a}=λ\overrightarrow{b}$(λ为非零实数)是否成立,若成立则说明共线,若不成立则说明不共线.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,0] | B. | [2,+∞) | C. | (-∞,0]∪[2,+∞) | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱柱ABCD-A1B1C1D1中,AB∥C1D1,AB1⊥BC,且AA1=AB.
如图,在四棱柱ABCD-A1B1C1D1中,AB∥C1D1,AB1⊥BC,且AA1=AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com