
 如图,在四棱柱ABCD-A1B1C1D1中,AB∥C1D1,AB1⊥BC,且AA1=AB.
如图,在四棱柱ABCD-A1B1C1D1中,AB∥C1D1,AB1⊥BC,且AA1=AB.分析 (1)由四棱柱的性质,可得CD∥C1D1,再由公理四可得AB∥CD,运用线面平行的判定定理即可得到证明;
(2)运用菱形的对角线垂直和线面垂直和面面垂直的判定定理,即可得证.
解答 证明:(1)四棱柱ABCD-A1B1C1D1中,侧面CDD1C1为平行四边形,
即有CD∥C1D1,又AB∥C1D1,
即有AB∥CD,
AB?平面A1DC,CD?平面A1DC,
即有AB∥平面A1DC;
(2)四棱柱ABCD-A1B1C1D1中,侧面ABB1A1为平行四边形,
又AA1=AB,则ABB1A1为菱形,
即有AB1⊥A1B,
又AB1⊥BC,A1B∩BC=B,
即有AB1⊥平面A1BC,
由于AB1?平面AB1B,
故平面AB1B⊥平面A1BC.
点评 本题考查线面平行的判定定理的运用和面面垂直的判定定理的运用,注意运用线线平行和线面垂直的判定定理,考查空间想象能力和逻辑推理能力,属于中档题.


 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:填空题
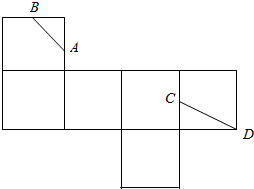 如图是一个正方体的平面展开图,A,B,C均为所在棱的中点,D为正方体的顶点,若正方体的棱长为2,则在正方体中,封闭折线ABCDA的长为3$\sqrt{2}+\sqrt{5}$.
如图是一个正方体的平面展开图,A,B,C均为所在棱的中点,D为正方体的顶点,若正方体的棱长为2,则在正方体中,封闭折线ABCDA的长为3$\sqrt{2}+\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
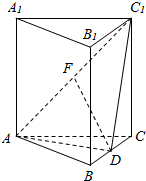 如图,在直三棱柱ABC-A1B1C1中,AB=AC,BD=DC,AF=C1F.
如图,在直三棱柱ABC-A1B1C1中,AB=AC,BD=DC,AF=C1F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不能作出这样的三角形 | B. | 能作出一个锐角三角形 | ||
| C. | 能作出一个直角三角形 | D. | 能作出一个钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$-1 | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\sqrt{3}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
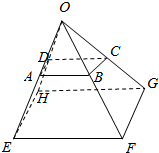 已知O、A、B、C、D、F、F、G、H为空间9个点(如图),并且$\overrightarrow{OE}$=k$\overrightarrow{OA}$,$\overrightarrow{OF}$=k$\overrightarrow{OB}$,$\overrightarrow{OH}$=k$\overrightarrow{OD}$,$\overrightarrow{AC}$=$\overrightarrow{AD}$+m$\overrightarrow{AB}$,$\overrightarrow{EG}$=$\overrightarrow{EH}$+m$\overrightarrow{EF}$.求证:
已知O、A、B、C、D、F、F、G、H为空间9个点(如图),并且$\overrightarrow{OE}$=k$\overrightarrow{OA}$,$\overrightarrow{OF}$=k$\overrightarrow{OB}$,$\overrightarrow{OH}$=k$\overrightarrow{OD}$,$\overrightarrow{AC}$=$\overrightarrow{AD}$+m$\overrightarrow{AB}$,$\overrightarrow{EG}$=$\overrightarrow{EH}$+m$\overrightarrow{EF}$.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com