
| AB |
| AC |
| PA |
| PB |
| PC |
| AB |
| AC |
λ2
|
| (2-2cosA)λ2+(2cosA-2)λ+1 |
| 2λ2-2λ+1 |
| 2 |
(2-2cosA)(λ-
|
|
| 2π |
| 3 |
| 3 |
| PA |
| PB |
| PC |
| 3 |
| 4 |
| ||
| 4 |
| 3 |
| 2 |
| AB |
| AC |
λ2
|
| 16λ2+4(2-2λ)2+2λ(2-2λ)×8cosA |
| (2-2cosA)λ2+(2cosA-2)λ+1 |
| 2λ2-2λ+1 |
2(λ-
|
| 2 |
(2-2cosA)(λ-
|
|
| 1 |
| 2 |
| 2π |
| 3 |
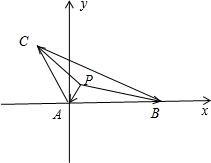 A(0,0),B(4,0),C(-1,
A(0,0),B(4,0),C(-1,| 3 |
| PC |
| PB |
| 3 |
| 3 |
| PA |
| PA |
| PB |
| PC |
| 3 |
| 3 |
| 3 |
| 4 |
| ||
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| ||
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| π |
| 2 |
| A、[-1+2k,1+2k],k∈Z | ||||
| B、[1+4k,3+4k],k∈Z | ||||
| C、[-1+4k,1+4k],k∈Z | ||||
D、[-1+4k+
|
查看答案和解析>>
科目:高中数学 来源: 题型:
2
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
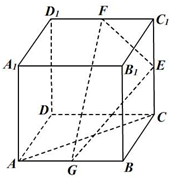 如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F,G分别为棱CC1,C1D1,AB的中点.
如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F,G分别为棱CC1,C1D1,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、若l⊥α,m?α,则l⊥m |
| B、若l⊥m,m?α,则l⊥α |
| C、若l∥α,m?α,则l∥m |
| D、若l∥α,m∥α,则l∥m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com