
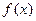 是定义在
是定义在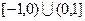 上的奇函数,当
上的奇函数,当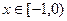 时,
时,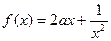 (a为实数).
(a为实数).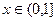 时,求
时,求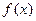 的解析式;
的解析式;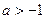 时,试判断
时,试判断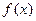 在
在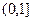 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.科目:高中数学 来源:不详 题型:解答题
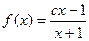 (
(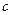 为常数).
为常数).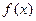 的零点, 求
的零点, 求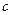 的值;
的值;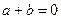 , 求
, 求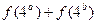 的值;
的值;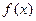 在[0,2]上的最大值为3, 求
在[0,2]上的最大值为3, 求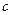 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(2,3) | B.(2,1) | C.(3,4) | D.(6,9) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 5件.
5件. 当该商场销售此服装的日销售量达到150件以上时,社会上就流行,问该款服装在社会上流行是否超过14天?并说明理由.
当该商场销售此服装的日销售量达到150件以上时,社会上就流行,问该款服装在社会上流行是否超过14天?并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com