练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图，P是椭圆上的一点，F是椭圆的左焦点，且，则点P到该椭圆左准线的距离为     ．
    【答案】分析：由可以推出Q是线段PF的中点，由P在椭圆上及，通过解方程组求得P点横坐标为，再求出到左准线的距离．
    解答：解：∵，
    ∴Q是线段PF的中点，
    ∵由P在椭圆上且，设P（a，b），F（-4，0），Q（），
    ∴，∴，
    椭圆左准线x=-．
    ∴点P到该椭圆左准线的距离．
    故答案：．
    点评：该题考查向量的线性表示以及椭圆的几何性质，另外还考查运算能力．是中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

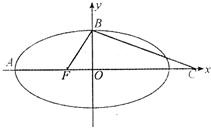    精英家教网如图，F是椭圆
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的一个焦点，A、B是椭圆的两个顶点，椭圆的离心率为
    1
    2
    ，点C在x轴上，BC⊥BF，由B、C、F三点确定的圆M恰好与直线x+
    		3
    y+3=0    相切．
    （I）求椭圆的方程；
    （II）过F作一条与两坐标轴都不垂直的直线l交椭圆于P、Q两点，若在x轴上存在一点N（x0，0），使得直线NP与直线NQ关于x轴对称，求x0的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•徐州一模）如图，在平面直角坐标系xOy中，椭圆E：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的焦距为2，且过点(
    		2
    ，
    		6
    2
    )    ．
    （1）求椭圆E的方程；
    （2）若点A，B分别是椭圆E的左、右顶点，直线l经过点B且垂直于x轴，点P是椭圆上异于A，B的任意一点，直线AP交l于点M．
    （ⅰ）设直线OM的斜率为k1，直线BP的斜率为k2，求证：k1k2为定值；
    （ⅱ）设过点M垂直于PB的直线为m．求证：直线m过定点，并求出定点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，P是双曲线
    x2
    a2
    -
    y2
    b2
    =1(a＞0，b＞0，xy≠0)    上的动点，F1、F2是双曲线的焦点，M是∠F1PF2的平分线上的一点，且
    F2M
    •
    MP
    =0    ．有一同学用以下方法研究|OM|：延长F2M交PF1于点N，可知△PNF2为等腰三角形，且M为F2N的中点，得|OM|=
    1
    2
    |NF1|=…=a    ．类似地：P是椭圆
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0，xy≠0)    上的动点，F1、F2是椭圆的焦点，M是∠F1PF2的平分线上的一点，且
    F2M
    •
    MP
    =0    ．则|OM|的取值范围是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

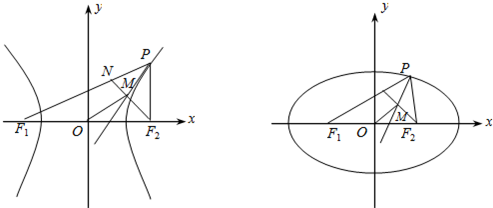
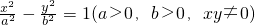    如图，P是双曲线数学公式上的动点，F1、F2是双曲线的焦点，M是∠F1PF2的平分线上的一点，且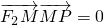数学公式．有一同学用以下方法研究|OM|：延长F2M交PF1于点N，可知△PNF2为等腰三角形，且M为F2N的中点，得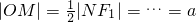数学公式．类似地：P是椭圆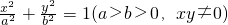数学公式上的动点，F1、F2是椭圆的焦点，M是∠F1PF2的平分线上的一点，且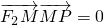数学公式．则|OM|的取值范围是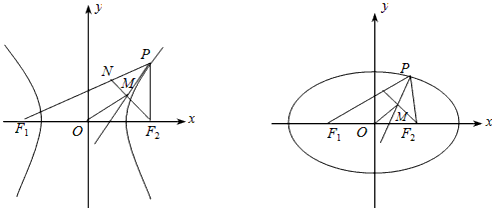


    1. A.
      数学公式
    2. B.
      数学公式
    3. C.
      数学公式
    4. D.
      数学公式

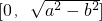
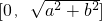
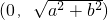
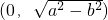
    查看答案和解析>>

    科目：高中数学 来源：2012年湖北省黄冈中学高三适应性考试数学试卷（理科）（解析版） 题型：选择题

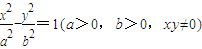    如图，P是双曲线上的动点，F1、F2是双曲线的焦点，M是∠F1PF2的平分线上的一点，且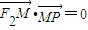．有一同学用以下方法研究|OM|：延长F2M交PF1于点N，可知△PNF2为等腰三角形，且M为F2N的中点，得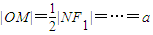．类似地：P是椭圆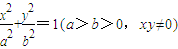上的动点，F1、F2是椭圆的焦点，M是∠F1PF2的平分线上的一点，且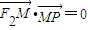．则|OM|的取值范围是（ ）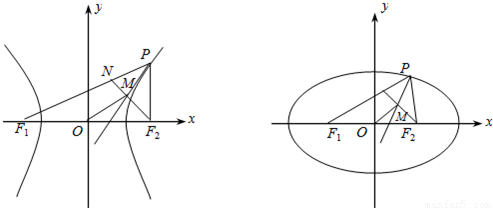
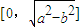
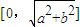
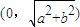
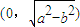
    A．
    B．
    C．
    D．

    查看答案和解析>>

    同步练习册答案