
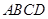 的边长为
的边长为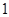 ,
,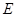 在
在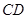 延长线上,且
延长线上,且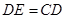 .动点
.动点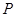 从点
从点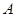 出发,沿正方形
出发,沿正方形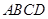 的边按逆时针方向运动一周回到
的边按逆时针方向运动一周回到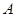 点,其中
点,其中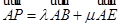 ,则下列命题正确的是 .(填上所有正确命题的序号)
,则下列命题正确的是 .(填上所有正确命题的序号)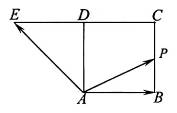
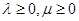 ;
;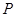 为
为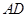 中点时,
中点时,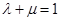 ;
;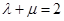 ,则点
,则点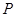 有且只有一个;
有且只有一个;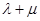 的最大值为
的最大值为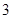 ;
;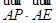 的最大值为
的最大值为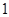 .
.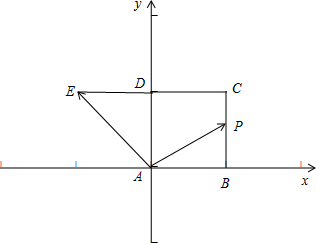
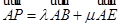
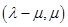 ,由图像可知
,由图像可知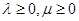 ,故①正确;
,故①正确;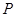 为
为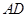 中点时,
中点时,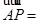
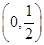 ,
,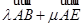 =
= 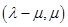 ,所以
,所以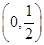 =
=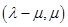 ,
, ,则
,则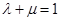 ,故②正确;
,故②正确;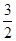 ,μ=
,μ=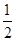 时,AP=(1,
时,AP=(1,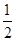 ),此时点P为BC的中点,满足λ+μ=2,
),此时点P为BC的中点,满足λ+μ=2,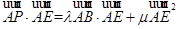 =
=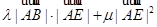 =
=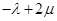 ,
,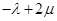 ≤0,
≤0,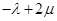 ≤0,
≤0,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
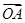 =(3,-4),
=(3,-4),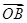 =(6,-3),
=(6,-3),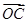 =(5-m,-3-m).
=(5-m,-3-m).查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
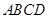 中,
中,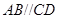 ,
,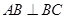 ,
,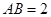 ,
,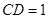 ,
,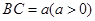 ,P为线段
,P为线段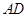 (含端点)上一个动点,设
(含端点)上一个动点,设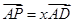 ,
,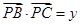 ,对于函数
,对于函数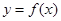 ,给出以下三个结论:①当
,给出以下三个结论:①当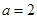 时,函数
时,函数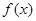 的值域为
的值域为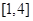 ;②对任意
;②对任意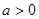 ,都有
,都有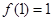 成立;③对任意
成立;③对任意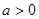 ,函数
,函数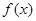 的最大值都等于4.④存在实数
的最大值都等于4.④存在实数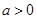 ,使得函数
,使得函数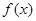 最小值为0 .其中所有正确结论的序号是_________.
最小值为0 .其中所有正确结论的序号是_________.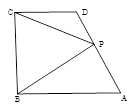
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
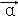 和
和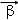 ,定义
,定义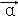 ○
○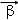 =
=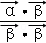 ,若平面向量
,若平面向量 、
、 满足|
满足| |≥|
|≥| |>0,
|>0, 与
与 的夹角
的夹角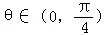 ,且
,且 ○
○ 和
和 ○
○ 都在集合
都在集合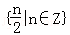 中,则
中,则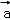 ○
○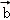 =( )
=( )A.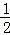 | B.1 | C.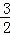 | D.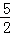 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
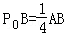 ,且对于边AB上任一点P,恒有
,且对于边AB上任一点P,恒有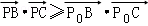 则( )
则( )| A.∠ABC=90° | B.∠BAC=90° | C.AB=AC | D.AC=BC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com