
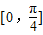 上单调递增的是( )
上单调递增的是( )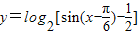


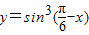
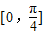 逐一检验即可得到答案.
逐一检验即可得到答案.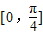 逐一检验知,
逐一检验知,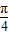 ]⇒x-
]⇒x-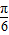 ∈[-
∈[-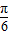 ,
,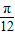 ],当x-
],当x-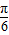 =-
=-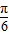 ⇒sin(x-
⇒sin(x- )-
)- =-1<0,不符合真数的要求,故A舍;
=-1<0,不符合真数的要求,故A舍;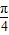 ]⇒2x+
]⇒2x+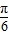 ∈[
∈[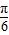 ,
,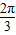 ],y=sin(2x+
],y=sin(2x+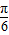 )在其上先增后减;整个函数也是先增后减,故B舍;
)在其上先增后减;整个函数也是先增后减,故B舍;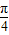 ]⇒2x-
]⇒2x-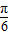 ∈[-
∈[-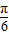 ,
,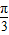 ],,满足根号内大于0以及递增的要求,故C符合要求;
],,满足根号内大于0以及递增的要求,故C符合要求;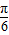 -x)=-sin3(x-
-x)=-sin3(x-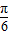 ),当x∈[0,
),当x∈[0, ]⇒x-
]⇒x-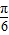 ∈[-
∈[-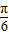 ,
,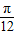 ],函数递减,故D不成立.
],函数递减,故D不成立.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2013-x2 |
| x2-2013 |
查看答案和解析>>
科目:高中数学 来源:2010年重庆市高一12月月考数学试卷 题型:解答题
(12分)已知函数 ,
,
(1)当 时,求
时,求 的反函数
的反函数 ;
;
(2)求关于 的函数
的函数 当
当 时的最小值
时的最小值 ;
;
(3)我们把同时满足下列两个性质的函数称为“和谐函数”: ①函数在整个定义域上是单调增函数或单调减函数;②在函数的定义域内存在区间
①函数在整个定义域上是单调增函数或单调减函数;②在函数的定义域内存在区间 使得函数在区间
使得函数在区间 上的值域为
上的值域为 .
.
 (Ⅰ)判断(2)中
(Ⅰ)判断(2)中 是否为“和谐函数”?若是,求出
是否为“和谐函数”?若是,求出 的值或关系式;若不是,请说明理由;
的值或关系式;若不是,请说明理由;
(Ⅱ)若关于 的函数
的函数 是“和谐函数”,求实数
是“和谐函数”,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(强化班) 下列说法中:
① 若定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,则函数
,则函数![]() 在
在![]() 上不是单调减函数;
上不是单调减函数;
② 定义在![]() 上的函数
上的函数![]() 在区间
在区间![]() 上是单调减函数,在区间
上是单调减函数,在区间![]() 上也是单调减函数,
上也是单调减函数,
则函数![]() 在
在![]() 上是单调减函数;
上是单调减函数;
③ 对于定义在![]() 上的函数
上的函数![]() ,若
,若![]() ,则
,则![]() 不可能是奇函数;
不可能是奇函数;
④ ![]() 既是奇函数又是偶函数.
既是奇函数又是偶函数.
其中正确说法的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com