
椭圆C: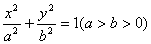 的离心率为
的离心率为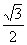 ,且过点(2,0)
,且过点(2,0)
(1)求椭圆C的方程;
(2)设直线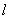 :
: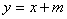 与椭圆C交于A.B两点,O为坐标原点,若
与椭圆C交于A.B两点,O为坐标原点,若 OAB为直角三角形,求
OAB为直角三角形,求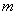 的值。
的值。
解(1)依题意,可知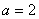 ,又
,又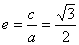 ,所以可知
,所以可知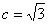
∴ 
故所求的椭圆方程为 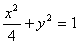 ……………………………………………3分
……………………………………………3分
(2)联立方程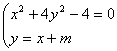 消去
消去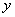 得
得 …………4分
…………4分
则 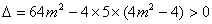
解得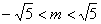
设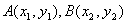
则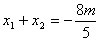 ,
,
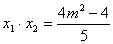 ………………5分
………………5分
① 若 ,则可知
,则可知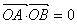 ,即
,即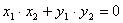
∴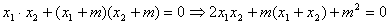
可解得
经检验 满足条件
满足条件
所以直线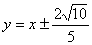 满足题意………………………………………9分
满足题意………………………………………9分
② 若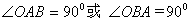 ,则
,则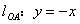 (或
(或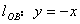 )
)
联立方程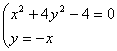
解得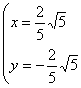 或
或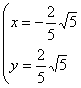 …………………10分
…………………10分
Ⅰ.若A(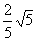 ,-
,-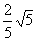 ) ,则可知
) ,则可知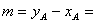 -
-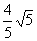
Ⅱ.若B(-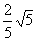 ,
, 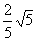 ) ,则可知
) ,则可知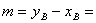
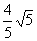
所以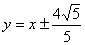 也满足题意…………………………………………………12分
也满足题意…………………………………………………12分
综上可知 ,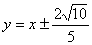 及
及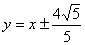 为所求的直线…………………13分
为所求的直线…………………13分
另解:② 若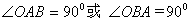 ,则
,则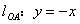 (或
(或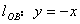 )
)
联立方程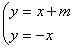 解得
解得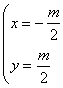 ,………………………………………………10分
,………………………………………………10分
则点(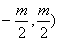 在
在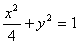 上,代入解得
上,代入解得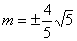 ,所以
,所以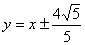 也满足题意
也满足题意
……………………………………………………………………………………………12分


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
已知椭圆C:![]() =1(
=1(![]() )的离心率为
)的离心率为![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,坐标原点
两点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求△
,求△![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2009年广东省广州市高考数学二模试卷(文科)(解析版) 题型:解答题
 的离心率为
的离心率为 ,且经过点
,且经过点 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省漳州市七校高三第三次联考文科数学试卷(解析版) 题型:解答题
已知椭圆C: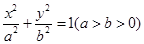 的离心率为
的离心率为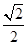 ,且经过点
,且经过点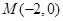 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设斜率为1的直线l与椭圆C相交于 ,
,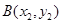 两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且
两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且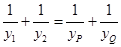 .求△ABM的面积.
.求△ABM的面积.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省高三第二次仿真测试文科数学试卷(解析版) 题型:解答题
已知椭圆C: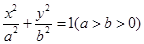 ,的离心率为
,的离心率为 ,A,B分别为椭圆的长轴和短轴的端点,M为AB的中点,O为坐标原点,且
,A,B分别为椭圆的长轴和短轴的端点,M为AB的中点,O为坐标原点,且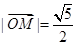 .
.
(1)求椭圆的方程;
(2)过(-1,0)的直线l与椭圆交于P、Q两点,求 POQ的面积的最大时直线l的方程。
POQ的面积的最大时直线l的方程。
查看答案和解析>>
科目:高中数学 来源:2013届福建省高二下学期第一次阶段考数学理科试卷 题型:解答题
已知椭圆C:
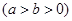 的离心率为
的离心率为 ,椭圆C上任意一点到椭圆两焦点的距离之和为6.
,椭圆C上任意一点到椭圆两焦点的距离之和为6.
(1)求椭圆C的方程;
(2)设直线 与椭圆C交于A,B两点,点P(0,1),且满足PA=PB,求直线
与椭圆C交于A,B两点,点P(0,1),且满足PA=PB,求直线 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com