
 对任意的
对任意的 上恒成立,则
上恒成立,则 的取值范围是( )
的取值范围是( )A. | B. | C. | D. |
 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源:不详 题型:解答题
 (其中点P、Q分别在边BC、CD上),搜索区域为平面四边形APCQ围成的海平面.设
(其中点P、Q分别在边BC、CD上),搜索区域为平面四边形APCQ围成的海平面.设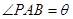 ,搜索区域的面积为
,搜索区域的面积为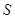 .
.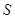 与
与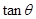 的关系式,并指出
的关系式,并指出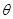 的取值范围;
的取值范围;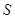 的最大值,并求此时
的最大值,并求此时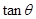 的值.
的值.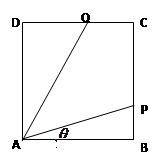
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
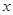 公里的相邻两增压站之间的输油管道费用为
公里的相邻两增压站之间的输油管道费用为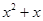 万元.设余下工程的总费用为
万元.设余下工程的总费用为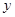 万元.
万元.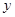 表示成
表示成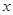 的函数;
的函数;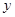 最小,其最小值为多少?
最小,其最小值为多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
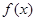 ,若存在实数对(
,若存在实数对(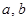 ),使得等式
),使得等式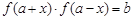 对定义域中的每一个
对定义域中的每一个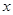 都成立,则称函数
都成立,则称函数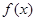 是“(
是“(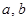 )型函数”.
)型函数”.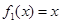 是否为 “(
是否为 “(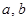 )型函数”,并说明理由;
)型函数”,并说明理由;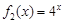 是“(
是“(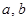 )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对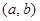 ;
;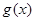 是“
是“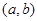 型函数”,对应的实数对
型函数”,对应的实数对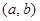 为
为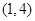 ,当
,当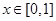 时,
时,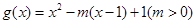 ,若当
,若当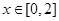 时,都有
时,都有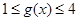 ,试求
,试求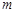 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.?x∈R,x2+2<2x | B.?x0∈Rx02+2≤2x0 |
| C.?x0∈RX02+2<2x0 | D.?x∈Rx2+2≤2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com