
分析 (1)求导数,利用f(x)在x=$\frac{3}{4}$处取得极值,即可求实数a的值;
(2)欲证f′($\frac{{x}_{1}+{x}_{2}}{2}$)>k,只须证明:$\frac{aln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}-{x}_{2}}$>$\frac{2a}{{x}_{1}+{x}_{2}}$,又$\frac{ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}-{x}_{2}}$>$\frac{2}{{x}_{1}+{x}_{2}}$?$\frac{2(\frac{{x}_{1}}{{x}_{2}}-1)}{\frac{{x}_{1}}{{x}_{2}}+1}$>ln$\frac{{x}_{1}}{{x}_{2}}$ 即需证明(1+$\frac{{x}_{1}}{{x}_{2}}$)ln$\frac{{x}_{1}}{{x}_{2}}$-2($\frac{{x}_{1}}{{x}_{2}}$-1)<0,令$\frac{{x}_{1}}{{x}_{2}}$=t∈(0,1),得到新函数,求导数,即可证明结论.
解答 (1)解:∵f′(x)=$\frac{2{x}^{2}-x-a}{x}$,f(x)在x=$\frac{3}{4}$处取得极值,
∴$\frac{1}{2}$-$\frac{4}{3}$a=0,解得a=$\frac{3}{8}$. …(2分)
经检验,当a=$\frac{3}{8}$时,函数f(x)在x=$\frac{3}{4}$处取得极小值.…(3分)
∴a=$\frac{3}{8}$;…(4分)
(2)证明:∵f′(x)=$\frac{2{x}^{2}-x-a}{x}$,
∴f′($\frac{{x}_{1}+{x}_{2}}{2}$)=x1+x2-$\frac{2a}{{x}_{1}+{x}_{2}}$-1
由题,k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=(x1+x2)-$\frac{aln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}-{x}_{2}}$-1 …(7分)
因为a>0,故欲证f′($\frac{{x}_{1}+{x}_{2}}{2}$)>k,只须证明:$\frac{aln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}-{x}_{2}}$>$\frac{2a}{{x}_{1}+{x}_{2}}$.…(8分)
又$\frac{ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}-{x}_{2}}$>$\frac{2}{{x}_{1}+{x}_{2}}$?$\frac{2(\frac{{x}_{1}}{{x}_{2}}-1)}{\frac{{x}_{1}}{{x}_{2}}+1}$>ln$\frac{{x}_{1}}{{x}_{2}}$ 即需证明(1+$\frac{{x}_{1}}{{x}_{2}}$)ln$\frac{{x}_{1}}{{x}_{2}}$-2($\frac{{x}_{1}}{{x}_{2}}$-1)<0 …(10分)
令$\frac{{x}_{1}}{{x}_{2}}$=t∈(0,1),则g(t)=(1+t)lnt-2t+2,g′(t)=lnt+$\frac{1}{t}$-1,g″(t)=$\frac{t-1}{{t}^{2}}$<0,
∴g′(t)在(0,1)上递减,∴g′(t)>g′(1)=0
∴g(t)在(0,1)上递增,
∴g(t)<g(1)=0,
∴(1+$\frac{{x}_{1}}{{x}_{2}}$)ln$\frac{{x}_{1}}{{x}_{2}}$-2($\frac{{x}_{1}}{{x}_{2}}$-1)<0成立,即f′($\frac{{x}_{1}+{x}_{2}}{2}$)>k.…(12分)
点评 本题考查导数知识的综合运用,考查函数的极值,考查不等式的证明,正确转化是关键.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
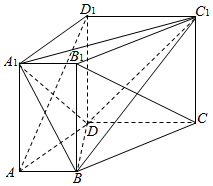 在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,∠ADC=90°,AB∥CD,AD=CD=DD1=2AB=2.
在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,∠ADC=90°,AB∥CD,AD=CD=DD1=2AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,16] | B. | (-∞,16) | C. | (16,+∞) | D. | [16,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
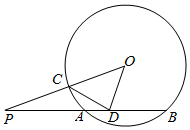 如图,割线PAB交于圆O于A、B两点,PO交于圆O于C,D在AB上,且满足CD2=DA•DB.
如图,割线PAB交于圆O于A、B两点,PO交于圆O于C,D在AB上,且满足CD2=DA•DB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
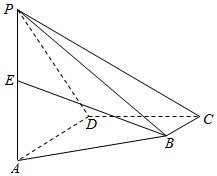 如图,四棱锥P-ABCD的底面是直角梯形,AD∥BC,∠ADC=90°,AD=2BC,PA⊥平面ABCD.
如图,四棱锥P-ABCD的底面是直角梯形,AD∥BC,∠ADC=90°,AD=2BC,PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
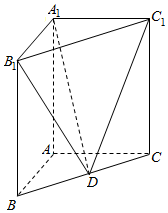 如图,在直三棱柱ABC-A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3.D是线段BC的中点.
如图,在直三棱柱ABC-A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3.D是线段BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com