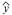练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    对有线性相关关系的两个变量建立的回归直线方程=+x中,回归系数(　　)
    A．不能小于0B．不能大于0
    C．不能等于0D．只能小于0
    C
    ∵=0时,相关系数r=0,这时不具有线性相关关系,但能大于0也能小于0.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    从某居民区随机抽取10个家庭,获得第个家庭的月收入(单位:千元)与月储蓄(单位:千元)的数据资料,算得
    ,,,.
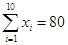    (1)求家庭的月储蓄对月收入的线性回归方程;
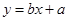    (2)判断变量与之间是正相关还是负相关;
    (3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
    其中,为样本平均值,线性回归方程也可写为
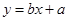    附:线性回归方程中,,,

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    改革开放以来，我国高等教育事业有了突飞猛进的发展，有人记录了某村2001到2005年五年间每年考入大学的人数，为了方便计算，2001年编号为1,2002年编号为2，……，2005年编号为5，数据如下：
    年份（x）
    		1
    		2
    		3
    		4
    		5
    人数（y）
    		3
    		5
    		8
    		11
    		13
    （1）从这5年中随机抽取两年，求考入大学的人数至少有年多于10人的概率.
    （2）根据这年的数据，利用最小二乘法求出关于的回归方程，并计算第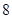年的估计值。
    参考:用最小二乘法求线性回归方程系数公式

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    一般来说，一个人脚越长，他的身高就越高．现对10名成年人的脚长x(单位：cm)与身高y(单位：cm)进行测量，得如下数据：
    x
    		20
    		21
    		22
    		23
    		24
    		25
    		26
    		27
    		28
    		29
    y
    		141
    		146
    		154
    		160
    		169
    		176
    		181
    		188
    		197
    		203
    作出散点图后，发现散点在一条直线附近．
    经计算得到一些数据：
    某刑侦人员在某案发现场发现一对裸脚印，量得每个脚印长26.5 cm，请你估计案发嫌疑人的身高为(    )
    A.185       B.185.5         C.186         D.186.5

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    关于线性回归,以下说法错误的是(　　)
    A．自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系
    B．在平面直角坐标系中用描点的方法得到的表示具有相关关系的两个变量的一组数据的图形叫做散点图
    C．线性回归直线方程最能代表观测值x,y之间的关系,且其回归直线一定过样本中心点(,)
    D．甲、乙、丙、丁四位同学各自对A,B两变量的线性相关性作试验,并由回归分析法分别求得相关系数rxy如下表
     
    		甲
    		乙
    		丙
    		丁
    rxy
    		0.82
    		0.78
    		0.69
    		0.85
    则甲同学的试验结果体现A,B两变量更强的线性相关性

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    某农场给某种农作物施肥量x(单位：吨)与其产量y(单位：吨)的统计数据如下表：
    施肥量x
    		2
    		3
    		4
    		5
    产量y
    		26
    		39
    		49
    		54
    根据上表，得到回归直线方程＝9.4x＋，当施肥量x＝6时，该农作物的预报产量是________．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知x与y之间的一组数据(如表所示)：则关于y与x的线性回归方程y＝bx＋a必过定点(　　)
    A．(2,2)B．(1.5,0)C．(1,2) D．(1.5,4)

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

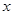    某商场在销售过程中投入的销售成本与销售额的统计数据如下表：
    销售成本x(万元)
    		3
    		4
    		6
    		7
    销售额（万元）
    		25
    		34
    		49
    		56
    根据上表可得，该数据符合线性回归方程：．由此预测销售额为100万元时，投入的销售成本大约为             ；

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    在研究硝酸钠的可溶性程度时,在不同的温度下观测它在水中的溶解度,得观测结果如下:
    温度(x)
    		0
    		10
    		20
    		50
    		70
    溶解度(y)
    		66.7
    		76.0
    		85.0
    		112.3
    		128.0
    则由此得到的回归直线的斜率是　　　　　　.

    查看答案和解析>>

    同步练习册答案