
科目:高中数学 来源: 题型:解答题
(本题满分13分)某工厂有214名工人, 现要生产1500件产品, 每件产品由3个A型零件与1个B型零件配套组成, 每个工人加工5个A型零件与3个B型零件所需时间相同. 现将全部工人分为两组, 分别加工一种零件, 同时开始加工. 设加工A型零件的工人有x人, 在单位时间内每人加工A型零件5k个(k∈N*), 加工完A型零件所需时间为g(x), 加工完B型零件所需时间为h (x).
(Ⅰ) 试比较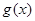 与
与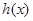 大小, 并写出完成总任务的时间
大小, 并写出完成总任务的时间 的表达式;
的表达式;
(Ⅱ) 怎样分组才能使完成任务所需时间最少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分16分)
已知 ,
,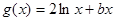 ,且直线
,且直线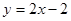 与曲线
与曲线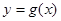 相切.
相切.
(1)若对 内的一切实数
内的一切实数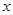 ,不等式
,不等式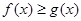 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)当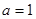 时,求最大的正整数
时,求最大的正整数 ,使得对
,使得对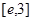 (
(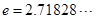 是自然对数的底数)内的任意
是自然对数的底数)内的任意 个实数
个实数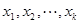 都有
都有 成立;
成立;
(3)求证: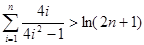
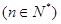 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
一种放射性元素,最初的质量为500g,按每年10﹪衰减.
(Ⅰ)求t年后,这种放射性元素质量ω的表达式;
(Ⅱ)由求出的函数表达式,求这种放射性元素的半衰期(剩留量为原来的一半所需要的时间).(精确到0.1;参考数据: )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
我市有甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.
(1)设在甲家租一张球台开展活动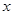 小时的收费为
小时的收费为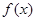 元
元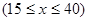 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动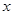 小时的收费为
小时的收费为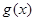 元
元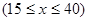 ,试求
,试求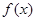 和
和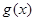 。
。
(2)问:小张选择哪家比较合算?说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com