
(本小题满分10分)
一种放射性元素,最初的质量为500g,按每年10﹪衰减.
(Ⅰ)求t年后,这种放射性元素质量ω的表达式;
(Ⅱ)由求出的函数表达式,求这种放射性元素的半衰期(剩留量为原来的一半所需要的时间).(精确到0.1;参考数据: )
)
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少.把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元.现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的价格(标价)出售. 问:
(1)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(2)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)="2" sin (0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点.
(0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点.
(1)求点A、B的坐标以及 ·
·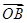 的值;
的值;
(2)没点A、B分别在角 、
、 的终边上,求tan(
的终边上,求tan(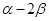 )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分16分)
有甲、乙两种商品,经销这两种商品所获的利润依次为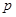 (万元)和
(万元)和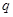 (万元),它们与投入的资金
(万元),它们与投入的资金 (万元)的关系,据经验估计为:
(万元)的关系,据经验估计为: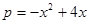 ,
, 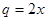 今有3万元资金投入经销甲、乙两种商品,为了获得最大利润,应对甲、乙两种商品分别投入多少资金?总共获得的最大利润是多少万元?
今有3万元资金投入经销甲、乙两种商品,为了获得最大利润,应对甲、乙两种商品分别投入多少资金?总共获得的最大利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂生产一种产品,已知该产品的月产量x吨与每吨产品的价格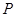 (元)之间的关系为
(元)之间的关系为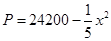 ,且生产
,且生产 吨的成本为
吨的成本为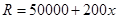 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知函数 =
=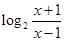 .
.
(1)判断函数 的奇偶性,并证明;
的奇偶性,并证明;
(2)求 的反函数
的反函数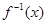 ,并求使得函数
,并求使得函数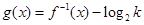 有零点的实数
有零点的实数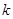 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com