
某工厂生产一种产品,已知该产品的月产量x吨与每吨产品的价格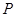 (元)之间的关系为
(元)之间的关系为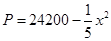 ,且生产
,且生产 吨的成本为
吨的成本为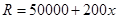 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
专家通过研究学生的学习行为,发现学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设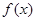 表示学生注意力随时间
表示学生注意力随时间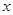 (分钟)的变化规律(
(分钟)的变化规律(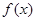 越大,表明学生注意力越大),经过试验分析得知:
越大,表明学生注意力越大),经过试验分析得知: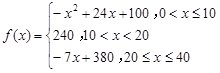
(Ⅰ)讲课开始后多少分钟,学生的注意力最集中?能坚持多少分钟?
(Ⅱ)讲课开始后5分钟时与讲课开始后25分钟时比较,何时学生的注意力更集中?
(Ⅲ)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲完这道题目?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元.该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(2)设一次订购量为x个,零件的实际出厂单价为P元,写出函数P=f(x)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)通常情况下,同一地区一天的温度随时间变化的曲线接近于函数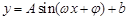 的图像.2013年1月下旬荆门地区连续几天最高温度都出现在14时,最高温度为
的图像.2013年1月下旬荆门地区连续几天最高温度都出现在14时,最高温度为 ;最低温度出现在凌晨2时,最低温度为零下
;最低温度出现在凌晨2时,最低温度为零下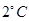 .
.
(Ⅰ)请推理荆门地区该时段的温度函数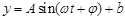
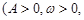
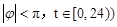 的表达式;
的表达式;
(Ⅱ)29日上午9时某高中将举行期末考试,如果温度低于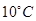 ,教室就要开空调,请问届时学校后勤应该送电吗?
,教室就要开空调,请问届时学校后勤应该送电吗?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
一种放射性元素,最初的质量为500g,按每年10﹪衰减.
(Ⅰ)求t年后,这种放射性元素质量ω的表达式;
(Ⅱ)由求出的函数表达式,求这种放射性元素的半衰期(剩留量为原来的一半所需要的时间).(精确到0.1;参考数据: )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分8分) 某车间生产某机器的两种配件A和B,生产配件A成本费y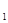 与该车间的工人人数x成反比,而生产配件B成本费y
与该车间的工人人数x成反比,而生产配件B成本费y 与该车间的工人人数x成正比,如果该车间的工人人数为10人时,这两项费用y
与该车间的工人人数x成正比,如果该车间的工人人数为10人时,这两项费用y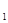 和y
和y 分别为2万元和8万元,那么要使这两项费用之和最小,该车间的工人人数x应为多少?
分别为2万元和8万元,那么要使这两项费用之和最小,该车间的工人人数x应为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分13分)某化工企业2012年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.设该企业使用该设备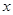 年的年平均污水处理费用为
年的年平均污水处理费用为 (万元)。
(万元)。
(1)用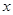 表示
表示 ;
;
(2)当该企业的年平均污水处理费用最低时,企业需重新更换新的污水处理设备.则该企业几年后需要重新更换新的污水处理设备。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)某单位用2 160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2 000平方米的楼房,经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com