
(本题满分13分)某化工企业2012年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.设该企业使用该设备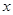 年的年平均污水处理费用为
年的年平均污水处理费用为 (万元)。
(万元)。
(1)用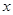 表示
表示 ;
;
(2)当该企业的年平均污水处理费用最低时,企业需重新更换新的污水处理设备.则该企业几年后需要重新更换新的污水处理设备。
科目:高中数学 来源: 题型:解答题
(本小题满分12分)南昌市在加大城市化进程中,环境污染问题也日益突出。据环保局测定,某处的污染指数与附近污染源的强度成正比,与到污染源距离的平方成反比.现已知相距18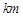 的A,B两家工厂(视作污染源)的污染强度分别为
的A,B两家工厂(视作污染源)的污染强度分别为 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数 等于两家工厂对该处的污染指数之和.设
等于两家工厂对该处的污染指数之和.设 (
(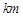 ).
).
(1) 试将 表示为
表示为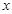 的函数;
的函数;
(2) 若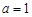 ,且
,且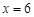 时,
时, 取得最小值,试求
取得最小值,试求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂生产一种产品,已知该产品的月产量x吨与每吨产品的价格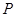 (元)之间的关系为
(元)之间的关系为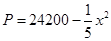 ,且生产
,且生产 吨的成本为
吨的成本为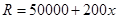 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分10分)
已知函数f (x)=| x-a | + | x + 2 |(a为常数,且a∈R).
(Ⅰ)若函数f (x)的最小值为2,求a的值;
(Ⅱ)当a=2时,解不等式f (x)≤6.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知函数 =
=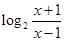 .
.
(1)判断函数 的奇偶性,并证明;
的奇偶性,并证明;
(2)求 的反函数
的反函数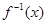 ,并求使得函数
,并求使得函数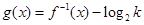 有零点的实数
有零点的实数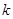 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分16分)
已知二次函数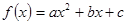 .
.
(1)设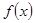 在
在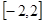 上的最大值、最小值分别是
上的最大值、最小值分别是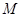 、
、 ,集合
,集合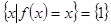 ,且
,且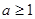 ,记
,记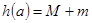 ,求
,求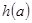 的最小值.
的最小值.
(2)当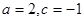 时,
时,
①设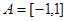 ,不等式
,不等式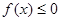 的解集为C,且
的解集为C,且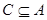 ,求实数
,求实数 的取值范围;
的取值范围;
②设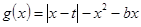
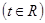 ,求
,求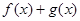 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com