
(本小题满分16分)
已知二次函数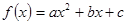 .
.
(1)设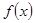 在
在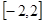 上的最大值、最小值分别是
上的最大值、最小值分别是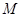 、
、 ,集合
,集合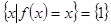 ,且
,且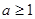 ,记
,记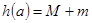 ,求
,求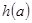 的最小值.
的最小值.
(2)当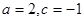 时,
时,
①设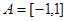 ,不等式
,不等式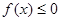 的解集为C,且
的解集为C,且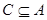 ,求实数
,求实数 的取值范围;
的取值范围;
②设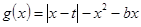
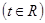 ,求
,求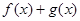 的最小值.
的最小值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
(本题满分13分)某化工企业2012年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.设该企业使用该设备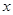 年的年平均污水处理费用为
年的年平均污水处理费用为 (万元)。
(万元)。
(1)用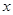 表示
表示 ;
;
(2)当该企业的年平均污水处理费用最低时,企业需重新更换新的污水处理设备.则该企业几年后需要重新更换新的污水处理设备。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)某单位用2 160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2 000平方米的楼房,经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分16分)某公司将进货单价为8元一个的商品按10元一个销售,每天可卖出100个,若这种商品的销售价每个上涨1元,则销售量就减少10个.
(1)求函数解析式;
(1)求销售价为13元时每天的销售利润;
(2)如果销售利润为360元,那么销售价上涨了几元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为1.80元;当用水超过4吨时,超过部分每吨3.00元。某月甲、乙两户共交水费 元,已知甲、乙两户该月用水量分别为
元,已知甲、乙两户该月用水量分别为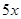 吨和
吨和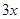 吨。
吨。
(1)求 关于
关于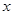 的函数;
的函数;
(2)若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量和水费。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com