
(本题满分16分)某公司将进货单价为8元一个的商品按10元一个销售,每天可卖出100个,若这种商品的销售价每个上涨1元,则销售量就减少10个.
(1)求函数解析式;
(1)求销售价为13元时每天的销售利润;
(2)如果销售利润为360元,那么销售价上涨了几元?
科目:高中数学 来源: 题型:解答题
(本小题满分16分)
已知二次函数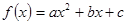 .
.
(1)设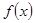 在
在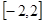 上的最大值、最小值分别是
上的最大值、最小值分别是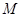 、
、 ,集合
,集合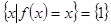 ,且
,且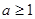 ,记
,记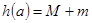 ,求
,求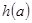 的最小值.
的最小值.
(2)当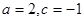 时,
时,
①设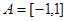 ,不等式
,不等式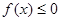 的解集为C,且
的解集为C,且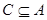 ,求实数
,求实数 的取值范围;
的取值范围;
②设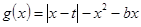
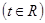 ,求
,求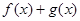 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题共12分)水库的蓄水量随时间而变化,现用t表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于t的近似函数关系式为
V(t)=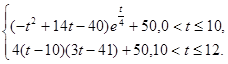
(Ⅰ)该水库的蓄水量小于50的时期称为枯水期.以i-1<t<i表示第i月份(i=1,2,…,12),问一年内哪几个月份是枯水期?
(Ⅱ)求一年内该水库的最大蓄水量(取e=2.7计算).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com