
(本小题满分14分)
已知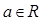 ,函数
,函数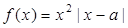 .
.
(Ⅰ)当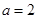 时,求使
时,求使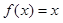 成立的
成立的 的集合;
的集合;
(Ⅱ)求函数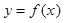 在区间
在区间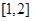 上的最小值.
上的最小值.
(Ⅰ) 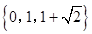 (Ⅱ)最小值为
(Ⅱ)最小值为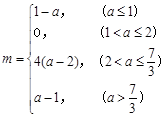
解析试题分析:(Ⅰ)由题意,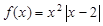 .
.
当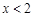 时,
时,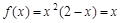 ,解得
,解得 或
或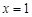 ;
;
当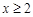 时,
时,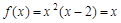 ,解得
,解得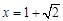 .
.
综上,所求解集为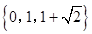 .
.
(Ⅱ)设此最小值为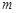 .
.
①当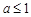 时,在区间
时,在区间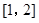 上,
上,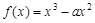 .
.
因为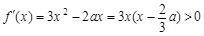 ,
,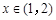 ,
,
则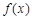 在区间
在区间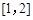 上是增函数,所以
上是增函数,所以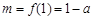 .
.
②当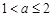 时,在区间
时,在区间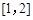 上,
上,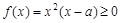 ,由
,由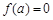 知
知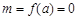 .
.
③当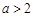 时,在区间
时,在区间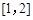 上,
上,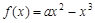 .
.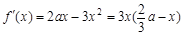 .
.
若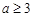 ,在区间
,在区间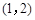 内
内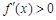 ,从而
,从而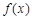 为区间
为区间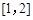 上的增函数,
上的增函数,
由此得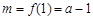 .
.
若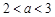 ,则
,则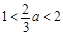 .
.
当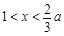 时,
时,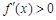 ,从而
,从而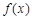 为区间
为区间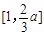 上的增函数;
上的增函数;
当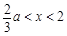 时,
时,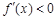 ,从而
,从而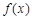 为区间
为区间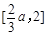 上的减函数.
上的减函数.
因此,当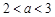 时,
时,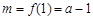 或
或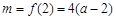 .
.
当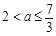 时,
时,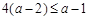 ,故
,故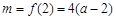 ;
;
当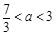 时,
时,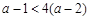 ,故
,故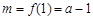 .
.
综上所述,所求函数的最小值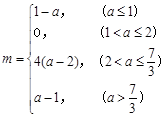
考点:本小题主要考查含绝对值的函数的最值的求法和利用导数求函数的最值,考查学生分类讨论思想的应用和运算求解能力.
点评:求解含绝对值的不等式或函数问题,关键是通过讨论去掉绝对值符号,讨论的时候要注意做到“不重不漏”.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:解答题
(本小题满分16分)
已知二次函数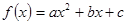 .
.
(1)设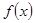 在
在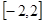 上的最大值、最小值分别是
上的最大值、最小值分别是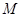 、
、 ,集合
,集合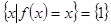 ,且
,且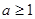 ,记
,记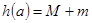 ,求
,求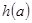 的最小值.
的最小值.
(2)当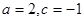 时,
时,
①设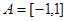 ,不等式
,不等式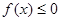 的解集为C,且
的解集为C,且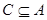 ,求实数
,求实数 的取值范围;
的取值范围;
②设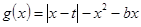
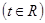 ,求
,求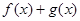 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题共12分)水库的蓄水量随时间而变化,现用t表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于t的近似函数关系式为
V(t)=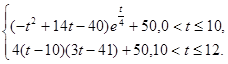
(Ⅰ)该水库的蓄水量小于50的时期称为枯水期.以i-1<t<i表示第i月份(i=1,2,…,12),问一年内哪几个月份是枯水期?
(Ⅱ)求一年内该水库的最大蓄水量(取e=2.7计算).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业为打入国际市场,决定从A、B两种产品中只选择一种进行投资生产.已
知投资生产这两种产品的有关数据如下表:(单位:万美元)
| 项目类别 | 年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多可生产的件数 |
| A产品 | 10 | m | 5 | 100 |
| B产品 | 20 | 4 | 9 | 60 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com