
【题目】已知![]() ,
,![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;(Ⅱ)
上单调递增;(Ⅱ)![]() .
.
【解析】
(Ⅰ)求函数导数,利用导数可研究函数的单调性;
(Ⅱ)由条件可得![]()
![]() 在
在![]() 上恒成立, 求导得
上恒成立, 求导得![]() ,分别讨论
,分别讨论![]() ,
,![]() 和
和![]() 三种情况,研究
三种情况,研究![]() 的最小值的取值情况,从而即可得解.
的最小值的取值情况,从而即可得解.
(Ⅰ)![]() 时,
时,![]() ,定义域是全体实数,求导得
,定义域是全体实数,求导得![]() ,
,
令![]() ,所以
,所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
(Ⅱ)令![]()
![]() 在
在![]() 上恒成立,则
上恒成立,则![]()
![]() 在
在![]() 上恒成立
上恒成立
求导得![]() .
.
若![]() ,显然
,显然![]() 可以任意小,不符合题意.
可以任意小,不符合题意.
若![]() ,则
,则![]() 最大也只能取0.
最大也只能取0.
当![]() 时,令
时,令![]()
![]() ,
,
于是![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递增,在
单调递增,在![]() 取唯一的极小值也是最小值
取唯一的极小值也是最小值
![]()
![]()
![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() .
.
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 单调递减,
单调递减,
在![]() 取唯一极大值也是最大值
取唯一极大值也是最大值![]() ,此时
,此时![]() ,
,![]() ,所以
,所以![]() 的最大值等于
的最大值等于![]() .
.
备注一:结合图象,指数函数在直线的上方,斜率![]() 显然,再讨论
显然,再讨论![]() 的情况.
的情况.
备注二:考虑到![]()
![]() 在
在![]() 上恒成立,令
上恒成立,令![]() 即得
即得![]() .取
.取![]() ,
,![]()
证明![]() 在
在![]() 上恒成立也给满分.
上恒成立也给满分.


科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元。
(1)分别写出两类产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,怎样分配资金才能获得最大收益?其最大收益为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后2次抛掷一枚骰子,将得到的点数分别记为![]() ,
,![]() .
.
(1)求直线![]() 与圆
与圆![]() 相切的概率;
相切的概率;
(2)将![]() ,
,![]() ,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有大小均匀的![]() 个小球,其中有红色球
个小球,其中有红色球![]() 个,编号分别为
个,编号分别为![]() ;白色球
;白色球![]() 个, 编号分别为
个, 编号分别为![]() , 从盒子中任取
, 从盒子中任取![]() 个小球(假设取到任何—个小球的可能性相同).
个小球(假设取到任何—个小球的可能性相同).
(1)求取出的![]() 个小球中,含有编号为
个小球中,含有编号为![]() 的小球的概率;
的小球的概率;
(2)在取出的![]() 个小球中, 小球编号的最大值设为
个小球中, 小球编号的最大值设为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是圆
是圆![]() :
:![]() 上一动点,线段
上一动点,线段![]() 与圆
与圆![]() :
:![]() 相交于点
相交于点![]() .直线
.直线![]() 经过
经过![]() ,并且垂直于
,并且垂直于![]() 轴,
轴,![]() 在
在![]() 上的射影点为
上的射影点为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设圆![]() 与
与![]() 轴的左、右交点分别为
轴的左、右交点分别为![]() ,
,![]() ,点
,点![]() 是曲线
是曲线![]() 上的点(点
上的点(点![]() 与
与![]() ,
,![]() 不重合),直线
不重合),直线![]() ,
,![]() 与直线
与直线![]() :
:![]() 分别相交于点
分别相交于点![]() ,
,![]() ,求证:以
,求证:以![]() 直径的圆经过定点.
直径的圆经过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 若命题![]() 均为真命题,则命题
均为真命题,则命题![]() 为真命题
为真命题
B. “若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ”
”
C. 在![]() ,“
,“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
D. 命题![]() “
“![]() ”的否定为
”的否定为![]() “
“![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设![]() 米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
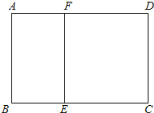
(1)求出y关于x的函数解析式及x的取值范围;
(2)当x为何值时,围墙(包括EF)的修建总费用y最小?并求出y的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com