
分析 两船如果能够相撞,那么他们横纵坐标相等式,由此能求出为了安全航行,避免两船相撞,系数k的取值范围.
解答 解:∵货轮S的位移向量沿坐标轴方向的分向量为S:$\left\{\begin{array}{l}{x=3+2t}\\{y=t-2}\end{array}\right.$,
汽艇B的位移向量沿坐标轴方向的分向量为:B:$\left\{\begin{array}{l}{x=4t-1}\\{y=kt+6}\end{array}\right.$,
∴两船如果能够相撞,那么的横纵坐标相等,
假设他们会相撞,则$\left\{\begin{array}{l}{3+2t=4t-1}\\{t-2=kt+6}\end{array}\right.$,
解得t=2,k=-3,
∴只有t=2时会相撞,此时k=-3,
∴为了安全航行,避免两船相撞,系数k的取值范围是{k|k≠-3}.
点评 本题考查系数的取值范围的求法,是中档题,解题时要认真审题,注意参数方程与普通方程互化公式的合理运用.


科目:高中数学 来源:2016-2017学年江西上高县二中高二文9月月考数学文试卷(解析版) 题型:解答题
已知直线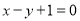 与圆
与圆 :
: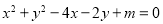 交于
交于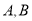 两点.
两点.
(1)求线段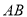 的垂直平分线的方程;
的垂直平分线的方程;
(2)若 ,求
,求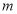 的值;
的值;
(3)在(2)的条件下,求过点 的圆
的圆 的切线方程。
的切线方程。
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川成都石室中学高二理下期中数学试卷(解析版) 题型:解答题
如图1,在等腰梯形 中,
中, ,
, 为
为 中点, 点
中点, 点 分别为
分别为 的中点, 将
的中点, 将 沿
沿 折起到
折起到  的位置,使得平面
的位置,使得平面 平面
平面 (如图
(如图  ).
).


(1)求证: ;
;
(2)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)侧棱 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川成都石室中学高二理下期中数学试卷(解析版) 题型:选择题
设 ,且
,且 ,“
,“ ”是“
”是“ ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {5,7} | B. | {2,4} | C. | {2,4,8} | D. | {1,3,5,6,7} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com