
分析 (1)消去参数,能直线l的普通方程,把P($\frac{1}{2}$,1)代入直线l的方程,能证明直线l过定点P($\frac{1}{2}$,1).由ρ2=x2+y2,ρcosθ=x,ρsinθ=y,能求出圆0的直角坐标方程.
(2)联立直线方程和圆的方程,我们可以得到一个关于t的方程,由于|t|表示P点到A,B的距离,故点P到A,B两点的距离之积为|t1•t2|,根据韦达定理,即可得到答案.
解答 解:(1)∵直线l的参数方程为$\left\{\begin{array}{l}{x=\frac{1}{2}+\frac{\sqrt{3}}{2}t}\\{y=1+\frac{1}{2}t}\end{array}\right.$ (t为参数),
∴消去参数,得直线l的普通方程为2x-2$\sqrt{3}$y+2$\sqrt{3}$-1=0.
把P($\frac{1}{2}$,1)代入直线l的方程,得:1-2$\sqrt{3}+2\sqrt{3}-1$=0,
∴直线l过定点P($\frac{1}{2}$,1).
∵圆0的极坐际方程为ρ=$\sqrt{2}$cos(θ-$\frac{π}{4}$)=$\sqrt{2}cosθcos\frac{π}{4}$+$\sqrt{2}sinθsin\frac{π}{4}$=cosθ+sinθ,
∴ρ2=ρcosθ+ρsinθ,
∴圆0的直角坐标方程为x2+y2-x-y=0.即$(x-\frac{1}{2})^{2}+(y-\frac{1}{2})^{2}=\frac{1}{2}$.
证明:(2)把直线l的参数方程$\left\{\begin{array}{l}{x=\frac{1}{2}+\frac{\sqrt{3}}{2}t}\\{y=1+\frac{1}{2}t}\end{array}\right.$代入$(x-\frac{1}{2})^{2}+(y-\frac{1}{2})^{2}=\frac{1}{2}$,
得${t}^{2}+\frac{1}{2}t-\frac{1}{4}$=0,
∴|PA|•|PB|=|t1t2|=$\frac{1}{4}$.
∴点P到A,B两点的距离之积为定值.
点评 本题考查的知识点是直线与圆的方程的应用,点的极坐标和直角坐标的互化,其中准确理解直线参数方程中参数的几何意义,极坐标方程中ρ,θ的几何意义,是解答本题的关键.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源:2015-2016学年四川成都石室中学高二文下期中数学试卷(解析版) 题型:选择题
设 ,且
,且 ,“
,“ ”是“
”是“ ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川成都石室中学高二理下期中数学试卷(解析版) 题型:选择题
过点 的直线与椭圆
的直线与椭圆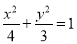 交于
交于 两点, 且点
两点, 且点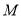 平分弦
平分弦 ,则直线
,则直线 的方程为( )
的方程为( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2kπ-$\frac{π}{6}$,2kπ+$\frac{π}{3}$](k∈Z) | B. | [2kπ+$\frac{π}{3}$,2kπ+$\frac{5π}{6}$](k∈Z) | ||
| C. | [kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$](k∈Z) | D. | [kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$](k∈Z) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com