
(2014•宿州三模)己知f(x)是定义在(0,+∞)上的单调函数,且?x∈(0,+∞),f[f(x)﹣lnx]=1,则方程f(x)+2x2f′(x)=7的解所在的区间为( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
C
【解析】
试题分析:由单调函数的性质,可得f(x)﹣lnx为定值,可以设t=f(x)﹣lnx,则f(x)=log2x+t,又由f(t)=3,可得f(x)的解析式,从而可化简方程,由二分法分析可得函数的零点所在的区间,结合函数的零点与方程的根的关系,即可得答案.
【解析】
根据题意,对任意的x∈(0,+∞),都有f[f(x)﹣lnx]=1,
又由f(x)是定义在(0,+∞)上的单调函数,
则f(x)﹣lnx为定值,
设t=f(x)﹣lnx,
则f(x)=lnx+t,
又由f(t)=1,
即lnt+t=1,
解得,t=1,
则f(x)=lnx+1,f′(x)= ,
,
∴f(x)+2x2f′(x)=lnx+2x=6,
即lnx+2x﹣6=0,
则方程f(x)+2x2f′(x)=6的解可转化成方程lnx+2x﹣6=0的解,
令h(x)=lnx+2x﹣6,
而h(2)=ln2﹣2<0,h(3)=ln3﹣1>0,
∴方程lnx+2x﹣6=0的解所在区间为(2,3),
∴方程f(x)+2x2f′(x)=7的解所在的区间为(2,3).
故选C.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:[同步]2014年湘教版选修2-3 8.4列联表独立性分析案例练习卷(解析版) 题型:?????
(2011•湖北)如图,用K、A1、A2三类不同的元件连接成一个系统.当K正常工作且A1、A2至少有一个正常工作时,系统正常工作,已知K、A1、A2正常工作的概率依次是0.9、0.8、0.8,则系统正常工作的概率为( )
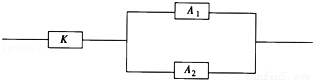
A.0.960 B.0.864 C.0.720 D.0.576
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-2 4.2导数的运算练习卷(解析版) 题型:?????
(2014•和平区三模)已知定义域为R的奇函数f(x)的导函数为f′(x),当x≠0时,f′(x)+ >0,若a=
>0,若a=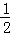 f(
f(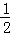 ),b=﹣2f(﹣2),c=(ln
),b=﹣2f(﹣2),c=(ln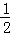 )f(ln
)f(ln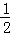 ),则a,b,c的大小关系正确的是( )
),则a,b,c的大小关系正确的是( )
A.a<c<b B.b<c<a C.a<b<c D.c<a<b
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-2 4.2导数的运算练习卷(解析版) 题型:?????
(2014•浙江模拟)已知f(x)为R上的可导函数,且满足f(x)>f′(x),对任意正实数a,下面不等式恒成立的是( )
A.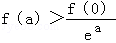
B.
C.f(a)>eaf(0)
D.f(a)<eaf(0)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-2 4.2导数的运算练习卷(解析版) 题型:?????
(2014•郑州模拟)已知f(x)=x2+2xf′(1),则f′(0)等于( )
A.0 B.﹣4 C.﹣2 D.2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.9共面与平行练习卷(解析版) 题型:?????
若平面α与β的法向量分别是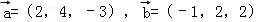 ,则平面α与β的位置关系是( )
,则平面α与β的位置关系是( )
A.平行 B.垂直 C.相交但不垂直 D.无法确定
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.5直线与平面的垂直关系练习卷(解析版) 题型:?????
(2011•朝阳区二模)已知棱长为1的正方体ABCD﹣A1B1C1D1中,点E,F分别是棱BB1,DD1上的动点,且BE=D1F=λ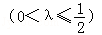 .设EF与AB所成的角为α,与BC所成的角为β,则α+β的最小值( )
.设EF与AB所成的角为α,与BC所成的角为β,则α+β的最小值( )
A.不存在 B.等于60 C.等于90 D.等于120
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.2空间中向量的概念和运算练习卷(解析版) 题型:?????
已知空间直角坐标系中A(1,1,0)且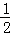 AB=(4,0,2),则B点坐标为( )
AB=(4,0,2),则B点坐标为( )
A.(9,1,4)
B.(9,﹣1,﹣4)
C.(8,﹣1,﹣4)
D.(8,1,4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com