
(2011•朝阳区二模)已知棱长为1的正方体ABCD﹣A1B1C1D1中,点E,F分别是棱BB1,DD1上的动点,且BE=D1F=λ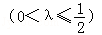 .设EF与AB所成的角为α,与BC所成的角为β,则α+β的最小值( )
.设EF与AB所成的角为α,与BC所成的角为β,则α+β的最小值( )
A.不存在 B.等于60 C.等于90 D.等于120
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源:2014-2015学年甘肃省高二上学期第四次月考理科数学试卷(解析版) 题型:选择题
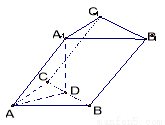
已知三棱柱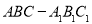 的侧棱与底面边长都相等,
的侧棱与底面边长都相等,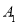 在底面
在底面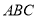 上的射影为
上的射影为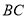 的中点,则异面直线
的中点,则异面直线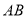 与
与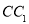 所成的角的余弦值为( )
所成的角的余弦值为( )
(A)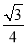 (B)
(B) (C)
(C)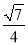 (D)
(D)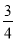
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-2 4.2导数的运算练习卷(解析版) 题型:?????
(2014•宿州三模)己知f(x)是定义在(0,+∞)上的单调函数,且?x∈(0,+∞),f[f(x)﹣lnx]=1,则方程f(x)+2x2f′(x)=7的解所在的区间为( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.9共面与平行练习卷(解析版) 题型:?????
已知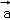 =(3λ+1,0,2λ),
=(3λ+1,0,2λ), =(1,λ﹣1,λ)若
=(1,λ﹣1,λ)若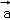 ⊥
⊥ ,则λ的值为( )
,则λ的值为( )
A.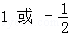 B.
B.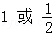 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.9共面与平行练习卷(解析版) 题型:?????
设平面α的法向量为(1,2,﹣2),平面β的法向量为(﹣2,﹣4,k),若α∥β,则k=( )
A.2 B.﹣4 C.4 D.﹣2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.5直线与平面的垂直关系练习卷(解析版) 题型:?????
(2012•安徽模拟)如图,已知三点A,B,E在平面α内,点C,D在α外,并且AC⊥α,DE⊥α,BD⊥AB.若AB=3,AC=BD=4,CD=5,则BD与平面α所成的角等于( )
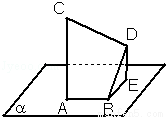
A.30° B.45° C.60° D.16°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.5直线与平面的垂直关系练习卷(解析版) 题型:?????
(2014•诸暨市模拟)已知点P是正方体ABCD﹣A1B1C1D1的表面上一动点,且满足|PA|=2|PB|,设PD1与平面ABCD所成角为θ,则θ的最大值为( )
A.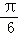 B.
B.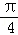 C.
C.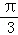 D.
D.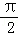
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.4直线的方向向量练习卷(解析版) 题型:填空题
已知等差数列{an}的前n次和为sn,且S2=10,S5=55,则过点P(n,an)和Q(n+2,an+2)(n∈﹣N*)的直线方向向量的坐标可以是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.1尝试用向量处理空间图形练习卷(解析版) 题型:?????
已知空间四边形OABC,其对角线OB、AC,M、N分别是边OA、CB的中点,点G在线段MN上,且使MG=2GN,用向量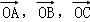 ,表示向量
,表示向量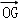 是( )
是( )
A.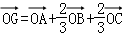
B.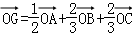
C.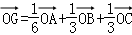
D.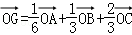
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com