
(2012•安徽模拟)如图,已知三点A,B,E在平面α内,点C,D在α外,并且AC⊥α,DE⊥α,BD⊥AB.若AB=3,AC=BD=4,CD=5,则BD与平面α所成的角等于( )
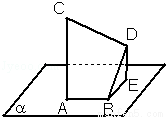
A.30° B.45° C.60° D.16°
A
【解析】
试题分析:根据DE⊥α,可得∠DBE是直线BD与平面α所成的角,然后过点D作DF⊥AC于F,连接AD,AE,可以证明出四边形AEDF为矩形,从而DE=AF.接下来用勾股定理计算出AD=5=CD,从而得到DF是△ACD的中线,即AF=CF=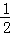 AC=2,最后在Rt△BDE中,利用三角函数的定义得到sin∠DBE=
AC=2,最后在Rt△BDE中,利用三角函数的定义得到sin∠DBE=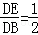 ,所以∠DBE=30°,可得直线BD与平面α所成的角等于30°.
,所以∠DBE=30°,可得直线BD与平面α所成的角等于30°.
【解析】
∵DE⊥α,
∴BE即为BD在平面α内的射影,
可得∠DBE是直线BD与平面α所成的角
过点D作DF⊥AC于F,连接AD,AE
∵AC⊥α,DE⊥α,
∴AC∥DE,且∠AED=∠FAE=∠DFA=90°
可得四边形AEDF为矩形
∴DE=AF
∵BD⊥AB
∴Rt△ABD中,AD=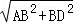 =
=
∵△ACD中,CD=AD=5
∴DF是中线,即AF=CF= AC=2
AC=2
∴Rt△BDE中,BD=4,DE=2
可得sin∠DBE=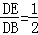
∴∠DBE=30°,即直线BD与平面α所成的角等于30°
故选A


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源:2014-2015学年甘肃省高二上学期第四次月考理科数学试卷(解析版) 题型:选择题
“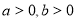 ”是“方程
”是“方程 表示椭圆”的
表示椭圆”的
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-2 4.2导数的运算练习卷(解析版) 题型:?????
(2014•郑州模拟)已知f(x)=x2+2xf′(1),则f′(0)等于( )
A.0 B.﹣4 C.﹣2 D.2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.9共面与平行练习卷(解析版) 题型:?????
已知A(2,1,1),B(1,1,2),C(2,0,1),则下列说法中正确的是( )
A.A,B,C三点可以构成直角三角形
B.A,B,C三点可以构成锐角三角形
C.A,B,C三点可以构成钝角三角形
D.A,B,C三点不能构成任何三角形
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.5直线与平面的垂直关系练习卷(解析版) 题型:?????
(2011•朝阳区二模)已知棱长为1的正方体ABCD﹣A1B1C1D1中,点E,F分别是棱BB1,DD1上的动点,且BE=D1F=λ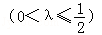 .设EF与AB所成的角为α,与BC所成的角为β,则α+β的最小值( )
.设EF与AB所成的角为α,与BC所成的角为β,则α+β的最小值( )
A.不存在 B.等于60 C.等于90 D.等于120
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.5直线与平面的垂直关系练习卷(解析版) 题型:?????
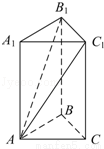
(2013•成都模拟)如图,在三棱柱ABC﹣A1B1C1中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则BB1与平面AB1C1所成的角是( )
A.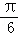 B.
B.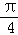 C.
C.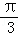 D.
D.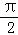
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.5直线与平面的垂直关系练习卷(解析版) 题型:?????
(2014•南宁二模)如图,在正三棱柱ABC﹣A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面AA1C1C所成角的正弦值为( )
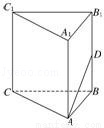
A.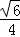 B.
B.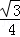 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.4直线的方向向量练习卷(解析版) 题型:选择题
若A(﹣1,0,1),B(1,4,7)在直线l上,则直线l的一个方向向量为( )
A.(1,2,3) B.(1,3,2) C.(2,1,3) D.(3,2,1)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.1尝试用向量处理空间图形练习卷(解析版) 题型:?????
已知空间四边形ABCD的对角线为AC、BD,设G是CD的中点,则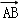 +
+ (
(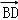 +
+ )等于( )
)等于( )
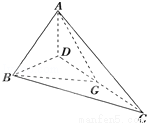
A. B.
B.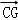 C.
C. D.
D.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com