
(2014•诸暨市模拟)已知点P是正方体ABCD﹣A1B1C1D1的表面上一动点,且满足|PA|=2|PB|,设PD1与平面ABCD所成角为θ,则θ的最大值为( )
A.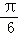 B.
B.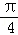 C.
C.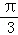 D.
D.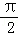
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:[同步]2014年湘教版选修2-3 8.4列联表独立性分析案例练习卷(解析版) 题型:?????
(2011•湖北)如图,用K、A1、A2三类不同的元件连接成一个系统.当K正常工作且A1、A2至少有一个正常工作时,系统正常工作,已知K、A1、A2正常工作的概率依次是0.9、0.8、0.8,则系统正常工作的概率为( )
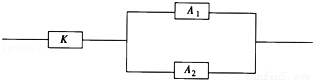
A.0.960 B.0.864 C.0.720 D.0.576
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.9共面与平行练习卷(解析版) 题型:?????
若平面α与β的法向量分别是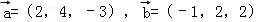 ,则平面α与β的位置关系是( )
,则平面α与β的位置关系是( )
A.平行 B.垂直 C.相交但不垂直 D.无法确定
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.5直线与平面的垂直关系练习卷(解析版) 题型:?????
(2011•朝阳区二模)已知棱长为1的正方体ABCD﹣A1B1C1D1中,点E,F分别是棱BB1,DD1上的动点,且BE=D1F=λ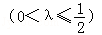 .设EF与AB所成的角为α,与BC所成的角为β,则α+β的最小值( )
.设EF与AB所成的角为α,与BC所成的角为β,则α+β的最小值( )
A.不存在 B.等于60 C.等于90 D.等于120
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.5直线与平面的垂直关系练习卷(解析版) 题型:?????
(2012•资阳三模)△ABC和△DBC所在的平面相互垂直,且AB=BC=BD,∠CBA=∠DBC=120°,则AD和平面BCD所成的角为( )
A.30° B.45° C.60° D.90°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.5直线与平面的垂直关系练习卷(解析版) 题型:?????
(2014•南宁二模)如图,在正三棱柱ABC﹣A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面AA1C1C所成角的正弦值为( )
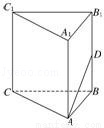
A.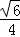 B.
B.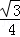 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.4直线的方向向量练习卷(解析版) 题型:填空题
直线l1:ax+2y+3a=0的方向向量恰为l2:3x+(a﹣5)y﹣2=0的一个法向量,则实数a的值为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.2空间中向量的概念和运算练习卷(解析版) 题型:?????
已知空间直角坐标系中A(1,1,0)且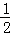 AB=(4,0,2),则B点坐标为( )
AB=(4,0,2),则B点坐标为( )
A.(9,1,4)
B.(9,﹣1,﹣4)
C.(8,﹣1,﹣4)
D.(8,1,4)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 2.4圆锥曲线的应用练习卷(解析版) 题型:?????
(2014•郑州一模)过双曲线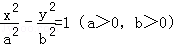 的左焦点F(﹣c,0),(c>0),作圆:x2+y2=
的左焦点F(﹣c,0),(c>0),作圆:x2+y2=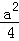 的切线,切点为E,延长FE交双曲线右支于点P,若
的切线,切点为E,延长FE交双曲线右支于点P,若 =
= (
(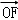 +
+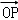 ),则双曲线的离心率为( )
),则双曲线的离心率为( )
A.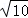 B.
B.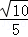 C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com