
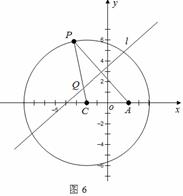
如图6,圆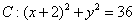 ,P是圆C上的任意一动点,A点坐标为(2,0),线段PA的垂直平分线l与半径CP交于点Q.
,P是圆C上的任意一动点,A点坐标为(2,0),线段PA的垂直平分线l与半径CP交于点Q.
(1)求点Q的轨迹G的方程;
(2)已知B,D是轨迹G上不同的两个任意点,M为BD的中点. ①若M的坐标为M(2,1),求直线BD所在的直线方程;②若BD不经过原点,且不垂直于x轴,点O为轨迹G的中心. 求证:直线BD和直线OM的斜率之积是常数(定值).
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
已知三次函数f(x)=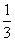 x3-(4m-1)x2+(15m2-2m-7)x+2在x∈(-∞,+∞)是增函数,则m的取值范围是( )
x3-(4m-1)x2+(15m2-2m-7)x+2在x∈(-∞,+∞)是增函数,则m的取值范围是( )
A.m<2或m>4 B.2≤m≤4
C.2<m<4 D. -4<m<-2
查看答案和解析>>
科目:高中数学 来源: 题型:
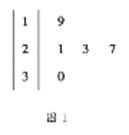
已知某篮球运动员2013年度参加了25场比赛,我从中抽取5场,用茎叶图统计该运动员5场 中的得分如图1所示,则该样本的方差为
A.25 B.24 C.18 D.16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com