
已知圆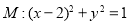 ,
,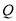 是直线
是直线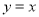 上的动点,
上的动点,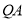 、
、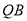 与圆
与圆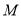 相切,切点分别为点
相切,切点分别为点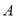 、
、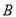 .
.
(1)若点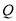 的坐标为
的坐标为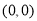 ,求切线
,求切线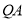 、
、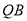 的方程;
的方程;
(2)若点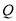 的坐标为
的坐标为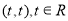 ,求直线
,求直线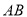 的方程.
的方程.
(1)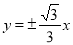 ;(2)
;(2)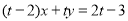
【解析】
试题分析:(1)在求直线方程时,应先选择恰当的直线方程的形式,并注意各种形式的适用条件,用斜截式及点斜式时,直线的斜率必须存在,而两点式不能表示与坐标轴垂直的直线,截距式不能表示与坐标轴垂直的直线或经过原点的直线,故在解题时,若采用截距式,应注意分类讨论,判断截距是否为零;若采用点斜式,应先考虑斜率不存在的情况;(2)根据圆的圆心坐标和半径求圆的标准方程,直线与圆相切时,圆心到直线的距离等于半径;(3)判断直线与圆的位置关系时,若两方程已知或圆心到直线的距离易表达,用几何法;若方程中含参数,或圆心到直线的距离的表达较繁琐,则用代数法.
试题解析:【解析】
(1)由题意可知当点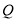 的坐标为(0,0)时,切线的斜率存在,可设切线方程为
的坐标为(0,0)时,切线的斜率存在,可设切线方程为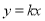 .
.
则圆心到切线的距离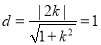 ,即
,即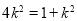 ,
,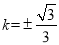 ,3分
,3分
∴切线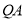 、
、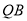 的方程为
的方程为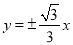 . 5分
. 5分
(2)设切线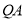 、
、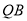 的切点为
的切点为 .
.
∵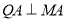 ,则切线
,则切线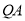 的斜率为
的斜率为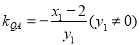 , 6分
, 6分
则切线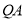 的方程为
的方程为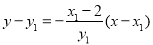 . 7分
. 7分
化简为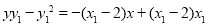 ,即
,即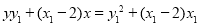
∵点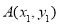 在圆
在圆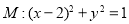 上,得
上,得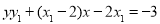 8分
8分
又∵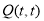 在切线
在切线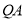 上,∴
上,∴ ①9分
①9分
同理得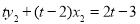 ②10分
②10分
由①②可知直线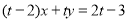 过点
过点
∴直线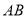 的方程为
的方程为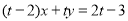 12分
12分
特别当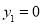 时,
时,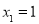 或
或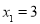
当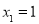 时切线
时切线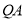 的方程为
的方程为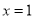 ,解得
,解得 ,得切点
,得切点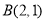
此时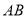 的方程为
的方程为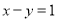 上式也成立
上式也成立
当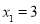 时得
时得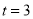 经检验方程也成立
经检验方程也成立
综上所述直线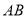 的方程为
的方程为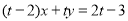 .14分
.14分
考点:(1)求切线方程;(2)点到直线的距离公式的应用;(3)直线方程的应用.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源:2016届浙江省温州市二外高一下学期期末考试数学试卷(解析版) 题型:选择题
设S n是公差为d(d≠0)的无穷等差数列{a n}的前n项和,则下列说法错误的是( )
A.若d<0,则数列{S n}有最大项
B.若数列{S n}有最大项,则d<0
C.若数列{S n}是递增数列,则对任意的n N*,均有S n>0
N*,均有S n>0
D.若对任意的n N*,均有S n>0,则数列{S n}是递增数列
N*,均有S n>0,则数列{S n}是递增数列
查看答案和解析>>
科目:高中数学 来源:2016届江苏省连云港市高一下学期期末数学试卷(三星)(解析版) 题型:填空题
某商场想通过检查发票及销售记录的2℅来快速估计每月的销售总额,现采用系统抽样,从某本50张的发票存根中随机抽取1张,如15号,然后按顺序往后抽,依次为15,65,115…,则第五个号是 .
查看答案和解析>>
科目:高中数学 来源:2015届青海省西宁市高三上学期第一次月考文科数学试卷(解析版) 题型:解答题
《选修4-4:坐标系与参数方程》已知直线L的参数方程: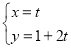 (t为参数)和圆C的极坐标方程:
(t为参数)和圆C的极坐标方程: 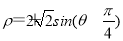 (θ为参数).
(θ为参数).
(1)求圆C的直角坐标方程.
(2)判断直线L和圆C的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com