
已知定义在 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,使得
,使得 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的上界.
的上界.
下面我们来考虑两个函数: ,
, .
.
(Ⅰ)当 时,求函数
时,求函数 在
在 上的值域,并判断函数
上的值域,并判断函数 在
在 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(Ⅱ)若 ,函数
,函数 在
在 上的上界是
上的上界是 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)若函数 在
在 上是以
上是以 为上界的有界函数, 求实数
为上界的有界函数, 求实数 的取值范围.
的取值范围.
(Ⅰ)函数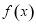 在
在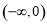 上的值域为
上的值域为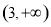 ,函数
,函数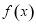 在
在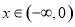 不是有界函数;(Ⅱ)
不是有界函数;(Ⅱ)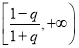 ;(Ⅲ)
;(Ⅲ)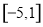 .
.
【解析】
试题分析:(Ⅰ)当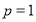 时,函数
时,函数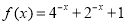 ,此时可设
,此时可设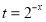 ,由
,由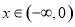 ,那么
,那么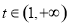 ,所以函数
,所以函数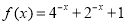 可转化成
可转化成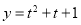 ,易知
,易知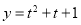 在
在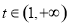 上单调递增,从而可求出值域为
上单调递增,从而可求出值域为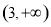 ;故不存在常数
;故不存在常数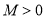 ,使
,使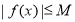 成立,所以函数
成立,所以函数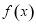 在
在 上不是有界函数
上不是有界函数
(Ⅱ)先求出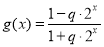 在
在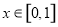 上的最大值
上的最大值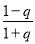 与最小值
与最小值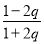 ,根据
,根据 ,再确定
,再确定
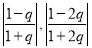 的大小关系,得出上界范围
的大小关系,得出上界范围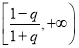 ;(Ⅲ)函数
;(Ⅲ)函数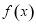 在
在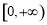 上是以
上是以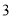 为上界的有界函数,则
为上界的有界函数,则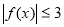 在
在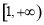 上恒成立.将问题转化成
上恒成立.将问题转化成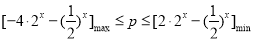 而求得
而求得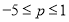 .
.
试题解析:(Ⅰ)当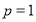 时,
时,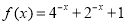
因为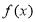 在
在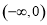 上递减,所以
上递减,所以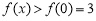 ,即
,即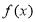 在
在 的值域为
的值域为 .
.
故不存在常数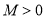 ,使
,使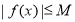 成立,所以函数
成立,所以函数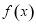 在
在 上不是有界函数.
上不是有界函数.
(Ⅱ)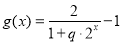 ,∵
,∵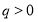 ,
,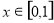 ∴
∴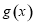 在
在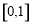 上递减,
上递减,
∴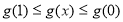 即
即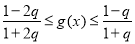
∵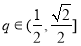 ,∴
,∴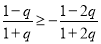 ,∴
,∴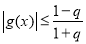 ,
,
∴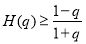 ,即
,即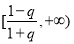
(Ⅲ)由题意知,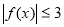 在
在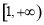 上恒成立.
上恒成立.
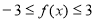 ,∴
,∴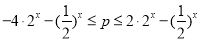 在
在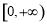 上恒成立
上恒成立
∴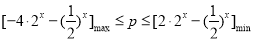
设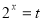 ,
,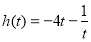 ,
,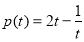 , 由
, 由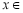
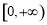 得
得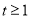 ,
,
设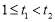 ,
,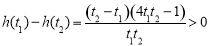 , 所以
, 所以 在
在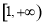 上递减,
上递减, 在
在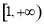 上的最大值为
上的最大值为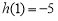 ,
,
又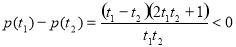 ,所以
,所以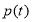 在
在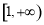 上递增,
上递增,
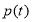 在
在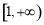 上的最小值为
上的最小值为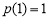 .
.
所以实数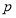 的取值范围为
的取值范围为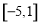 .
.
考点:信息检索,函数综合应用.


科目:高中数学 来源:2016届海南琼海市高一上学期段考数学试卷(解析版) 题型:选择题
同时满足以下三个条件的函数是( )
①图像过点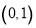 ;②在区间
;②在区间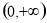 上单调递减③是偶函数 .
上单调递减③是偶函数 .
A、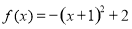 B、
B、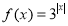
C、 D、
D、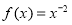
查看答案和解析>>
科目:高中数学 来源:2016届浙江省杭州市高一上学期抽测数学试卷(解析版) 题型:选择题
若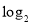 a<0,
a<0,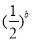 >1,则( )
>1,则( )
(A)a>1,b>0 (B)a>1,b<0 (C)0<a<1,b>0 (D)0<a<1,b<0
查看答案和解析>>
科目:高中数学 来源:2016届河南省郑州市高一上学期期末考试数学试卷(解析版) 题型:解答题
某商场经营一批进价是30元/件的商品,在市场试销中发现,此商品销售价 元与日销售量
元与日销售量 件之间有如下关系:
件之间有如下关系:
x | 45 | 50 |
y | 27 | 12 |
(I)确定 与
与 的一个一次函数关系式
的一个一次函数关系式 ;
;
(Ⅱ)若日销售利润为P元,根据(I)中关系写出P关于 的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?
的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com