
【题目】如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ
(1)试将由A到C所用的时间t表示为θ的函数t(θ);
(2)问θ为多少时,由A到C所用的时间t最少?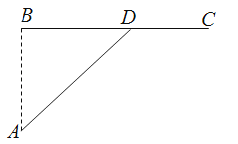
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某种大型商品,A,B两地都有出售,且价格相同、某地居民从两地之一购得商品后运回的费用是:每单位距离A地的运费是B地的运费的3倍,已知A,B两地距离为10千米,顾客选择A或B地购买这种商品的标准是:包括运费和价格的总费用较低,求A,B两地的售货区域的分界线的曲线形状,并指出曲线上、曲线内、曲线外的居民应如何选择购货地点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组函数表示同一函数的是( )
A.![]() 与y=x+3
与y=x+3
B.![]() 与y=x﹣1
与y=x﹣1
C.y=x0(x≠0)与y=1(x≠0)
D.y=2x+1,x∈Z与y=2x﹣1,x∈Z
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x和支出的维修费用y(万元),有如下表的统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系,试求:
(1)线性回归方程 ![]() .
.
(2)估计使用年限为10年时,维修费用是多少.
(3)计算总偏差平方和、残差平方和及回归平方和.
(4)求 ![]() 并说明模型的拟合效果.
并说明模型的拟合效果.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海上某货轮在A处看灯塔B在货轮的北偏东75°,距离为12![]() 海里;在A处看灯塔C在货轮的北偏西30°,距离为8
海里;在A处看灯塔C在货轮的北偏西30°,距离为8![]() 海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.(要画图)
海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.(要画图)
(1)A处与D处之间的距离;
(2)灯塔C与D处之间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4—4:坐标系与参数方程】
将圆![]() 上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(Ⅰ)写出C的参数方程;
(Ⅱ)设直线![]() 与C的交点为
与C的交点为![]() ,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段![]() 的中点且与
的中点且与![]() 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,☉O内切于△ABC的边于点D,E,F,AB=AC,连接AD交☉O于点H,直线HF交BC的延长线于点G. 
(1)求证:圆心O在AD上;
(2)求证:CD=CG;
(3)若AH∶AF=3∶4,CG=10,求HF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com