
分析 (1)利用条件,可知函数的对称轴为x=-1,最小值1-$\frac{{b}^{2}}{4a}$=0,代入可解;
(2)求出函数表达式f(x)=x2+bx,问题可转换为b≤$\frac{1}{x}$-x且b≥-$\frac{1}{x}$-x在(0,1]上恒成立,再转换为最值问题解出b的范围.
解答 解:(1)∵f(0)=1
∴c=1,
∵f(-1-x)=f(-1+x),f(x)min=0
∴对称轴为x=-1,
∴-$\frac{b}{2a}$=-1,1-$\frac{{b}^{2}}{4a}$=0
∴a=1,b=2
∴f(x)=(x+1)2…(7分)
(2)由题知,f(x)=x2+bx,
∴原命题等价于-1≤x2+bx≤1在(0,1]上恒成立,
即b≤$\frac{1}{x}$-x且b≥-$\frac{1}{x}$-x在(0,1]上恒成立.
又x∈(0,1]时,$\frac{1}{x}$-x的最小值为0,-$\frac{1}{x}$-x的最大值为-2,
∴-2≤b≤0.即b的取值范围是[-2,0]…(7分)
点评 考察了二次函数表达式的求法和恒成立问题的转换,属于常规题型,应熟练掌握解题方法.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$(a+b+1) | B. | $\frac{1}{2}$(a+b)+1 | C. | $\frac{1}{3}$(a+b+1) | D. | $\frac{1}{2}$a+b+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
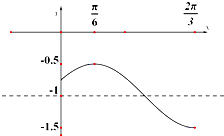 如果函数y=Asin(ωx+φ)+B(A>0,|φ|<$\frac{π}{2}$)的一段图象.
如果函数y=Asin(ωx+φ)+B(A>0,|φ|<$\frac{π}{2}$)的一段图象.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinα<sinβ | B. | cosα<sinβ | C. | cosα<cosβ | D. | cosα>cosβ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p | B. | 12p | C. | $\frac{{(1+p)}^{12}-12p-1}{12p}$ | D. | (1+p)12-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com