
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 5 | ||
女 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由;
下面的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式![]() 其中
其中![]() )
)
 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】(本小题10分)选修4—4:坐标系与参数方程
已知曲线C1的参数方程为![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ。
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ。
(Ⅰ)把C1的参数方程化为极坐标方程;
(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家规定,疫苗在上市前必须经过严格的检测,并通过临床实验获得相关数据,以保证疫苗使用的安全和有效.某生物制品硏究所将某一型号疫苗用在动物小白鼠身上进行科研和临床实验,得到统计数据如下:
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 40 |
|
|
注射疫苗 | 60 |
|
|
总计 | 100 | 100 | 200 |
现从未注射疫苗的小白鼠中任取1只,取到“感染病毒”的小白鼠的概率为![]() .
.
(Ⅰ)求![]() 列联表中的数据
列联表中的数据![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(Ⅱ)能否有![]() 把握认为注射此种疫苗有效?
把握认为注射此种疫苗有效?
(Ⅲ)在感染病毒的小白鼠中,按未注射疫苗和注射疫苗的比例抽取5只进行病例分析,然后从这五只小白鼠中随机抽取3只对注射疫苗情况进行核实,求至少抽到2只为未注射疫苗的小白鼠的概率.
附:![]() ,
,![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的空间几何体中,平面![]() 平面
平面![]() ,
,![]() 与
与![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() ,BE和平面ABC所成的角为
,BE和平面ABC所成的角为![]() ,且点E在平面ABC上的射影落在
,且点E在平面ABC上的射影落在![]() 的平分线上.
的平分线上.
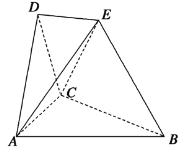
(1)求证:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知|x|≤2,|y|≤2,点P的坐标为(x,y).
(1)求当x,y∈R时,P满足(x-2)2+(y-2)2≤4的概率.
(2)求当x,y∈Z时,P满足(x-2)2+(y-2)2≤4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]()
![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() ,
,![]() 的公共点为
的公共点为![]() .
.
(Ⅰ)求直线![]() 的斜率;
的斜率;
(Ⅱ)若点![]() 分别为曲线
分别为曲线![]() ,
,![]() 上的动点,当
上的动点,当![]() 取最大值时,求四边形
取最大值时,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知实数![]() ,
,![]() ,
,![]() ,则
,则![]() 的最小值是______.
的最小值是______.
(2)正项等比数列![]() 中,存在两项
中,存在两项![]() 使得
使得![]() ,且
,且![]() ,则
,则![]() 的最小值为______.
的最小值为______.
(3)设正实数![]() 满足
满足![]() ,则
,则![]() 的最小值为_______.
的最小值为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]()
![]() Ⅰ
Ⅰ![]() 求椭圆
求椭圆![]() 的标准方程;
的标准方程;
![]() Ⅱ
Ⅱ![]() 已知抛物线
已知抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的右焦点重合,过点
的右焦点重合,过点![]() 的动直线与抛物线
的动直线与抛物线![]() 相交于A,B两个不同的点,在线段AB上取点Q,满足
相交于A,B两个不同的点,在线段AB上取点Q,满足![]() ,证明:点Q总在定直线上.
,证明:点Q总在定直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com