[题目]在高校自主招生中.某学校获得5个推荐名额.其中清华大学2名.北京大学2名.复旦大学1名．并且北京大学和清华大学都要求必须有男生参加．学校通过选拔定下3男2女共5个推荐对象.则不同的推荐方法共有( )A.20种B.22种C.24种D.36种题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】在高校自主招生中，某学校获得5个推荐名额，其中清华大学2名，北京大学2名，复旦大学1名．并且北京大学和清华大学都要求必须有男生参加．学校通过选拔定下3男2女共5个推荐对象，则不同的推荐方法共有（）
A.20种
B.22种
C.24种
D.36种

【答案】C
【解析】解：根据题意，分2种情况讨论：
①、第一类三个男生每个大学各推荐一人，两名女生分别推荐北京大学和清华大学，
共有 =12种推荐方法；
②、将三个男生分成两组分别推荐北京大学和清华大学，其余2个女生从剩下的2个大学中选，
共有 =12种推荐方法；
故共有12+12=24种推荐方法；
故选：C．
根据题意，分2种情况讨论：①、第一类三个男生每个大学各推荐一人，两名女生分别推荐北京大学和清华大学；②、将三个男生分成两组分别推荐北京大学和清华大学，其余2个女生从剩下的大学中选；分别求出每种情况下的推荐方法数目，由加法原理将其数目相加即可得答案．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知向量 =（m，﹣1）， =（）
（1）若m=﹣ ，求与的夹角θ；
（2）设． ①求实数m的值；
②若存在非零实数k，t，使得[ +（t2﹣3） ]⊥（﹣k +t ），求的最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，经过村庄A有两条互相垂直的笔直公路AB和AC，根据规划拟在两条公路围成的直角区域内建一工厂P，为了仓库存储和运输方便，在两条公路上分别建两个仓库M，N（异于村庄A，将工厂P及仓库M，N近似看成点，且M，N分别在射线AB，AC上），要求MN=2，PN=1（单位：km），PN⊥MN．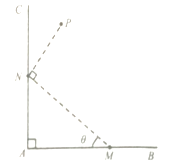
（1）设∠AMN=θ，将工厂与村庄的距离PA表示为θ的函数，记为l（θ），并写出函数l（θ）的定义域；
（2）当θ为何值时，l（θ）有最大值？并求出该最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知t为实数，函数f（x）=2loga（2x+t﹣2），g（x）=logax，其中0＜a＜1．
（1）若函数y=g（ax+1）﹣kx是偶函数，求实数k的值；
（2）当x∈[1，4]时，f（x）的图象始终在g（x）的图象的下方，求t的取值范围；
（3）设t=4，当x∈[m，n]时，函数y=|f（x）|的值域为[0，2]，若n﹣m的最小值为，求实数a的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设F（0，1），点P在x轴上，点Q在y轴上， =2 ， ⊥ ，当点P在x轴上运动时，点N的轨迹为曲线C．
（1）求曲线C的方程；
（2）过点F的直线l交曲线C于A，B两点，且曲线C在A，B两点处的切线相交于点M，若△MAB的三边成等差数列，求此时点M到直线AB的距离．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知命题p：点M（1，3）不在圆（x+m）2+（y﹣m）2=16的内部，命题q：“曲线表示焦点在x轴上的椭圆”，命题s：“曲线表示双曲线”．
（1）若“p且q”是真命题，求m的取值范围；
（2）若q是s的必要不充分条件，求t的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆C：9x2+y2=m2（m＞0），直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M．
（1）证明：直线OM的斜率与l的斜率的乘积为定值；
（2）若l过点（，m），延长线段OM与C交于点P，四边形OAPB能否为平行四边形？若能，求此时l的斜率；若不能，说明理由．