[题目]在下列四个命题中.错误的有( )A.坐标平面内的任何一条直线均有倾斜角和斜率B.直线的倾斜角的取值范围是C.若一条直线的斜率为.则此直线的倾斜角为D.若一条直线的倾斜角为.则此直线的斜率为题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】在下列四个命题中，错误的有（）

A.坐标平面内的任何一条直线均有倾斜角和斜率

B.直线的倾斜角的取值范围是

C.若一条直线的斜率为，则此直线的倾斜角为

D.若一条直线的倾斜角为，则此直线的斜率为

【答案】ACD

【解析】

A中，直线与轴垂直时，直线的倾斜角为，斜率不存在

B中，直线倾斜角的取值范围是

C中，直线的斜率为时，它的倾斜角不一定为

D中，直线的倾斜角为时，它的斜率为或不存在

对于A，当直线与轴垂直时，直线的倾斜角为，斜率不存在，A错误

对于B，直线倾斜角的取值范围是，B正确

对于C，一条直线的斜率为，此直线的倾斜角不一定为，

如的斜率为，它的倾斜角为，C错误

对于D，一条直线的倾斜角为时,它的斜率为或不存在，D错误

故选：ACD

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，在斜三棱柱中，底面是边长为2的正三角形，侧棱长为，点在底面的投影是线段的中点，为侧棱的中点.

（1）求证：平面；

（2）求平面与平面所成二面角的正弦值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】下面四个命题：

①在定义域上单调递增；

②若锐角，满足，则；

③是定义在上的偶函数，且在上是增函数，若，则；

④函数的一个对称中心是；

其中真命题的序号为______.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知二次函数满足（），且．

（1）求的解析式；

（2）若函数在区间上是单调函数，求实数的取值范围；

（3）若关于的方程有区间上有一个零点，求实数的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】圆O：x2+y2＝8内有一点P（﹣1，2），AB为过点P且倾斜角为α的弦，

（1）当α＝135°时，求AB的长；

（2）当弦AB被点P平分时，写出直线AB的方程．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知抛物线的焦点为，为坐标原点，是抛物线上异于的两点．

（1）求抛物线的方程；

（2）若直线的斜率之积为，求证：直线过定点．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知圆与轴负半轴相交于点，与轴正半轴相交于点.

（1）若过点的直线被圆截得的弦长为，求直线的方程；

（2）若在以为圆心半径为的圆上存在点，使得 (为坐标原点)，求的取值范围；

（3）设是圆上的两个动点，点关于原点的对称点为，点关于轴的对称点为，如果直线与轴分别交于和，问是否为定值？若是求出该定值；若不是，请说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在如图所示的几何体中，四边形CDEF为正方形，四边形ABCD为梯形，，，，平面ABCD．

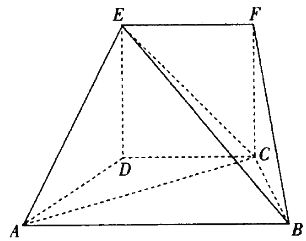
求BE与平面EAC所成角的正弦值；

线段BE上是否存在点M，使平面平面DFM？若存在，求的值；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为缓减人口老年化带来的问题，中国政府在2016年1月1日作出全国统一实施全面的“二孩”政策，生“二孩”是目前中国比较流行的元素某调查机构对某校学生做了一个是否同意父母生“二孩”抽样调查，该调查机构从该校随机抽查了100名不同性别的学生，调查统计他们是同意父母生“二孩”还是反对父母生“二孩”现已得知100人中同意父母生“二孩”占，统计情况如表：