
����Ŀ��ij��ѧ��֯�˵���֪ʶ�������Ӳμӿ��Ե�ѧ���г��40��ѧ��������ɼ�����Ϊ�������ֳ�����![]() ��
��![]() ������
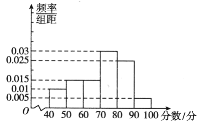
������![]() ���䲿��Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ���۲�ͼ�Σ��ش��������⣮
���䲿��Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ���۲�ͼ�Σ��ش��������⣮

��1����ɼ���![]() ��Ƶ�ʣ�����ȫ���Ƶ�ʷֲ�ֱ��ͼ��
��Ƶ�ʣ�����ȫ���Ƶ�ʷֲ�ֱ��ͼ��
��2��������ο��Եļ����ʣ�60�ּ�����Ϊ����ƽ���֣�������ʱ����������ֵ����������ݵ�ƽ��ֵ��
��3���ӳɼ���![]() ��
��![]() ��ѧ����ѡ���ˣ���������ͬһ�����εĸ��ʣ�
��ѧ����ѡ���ˣ���������ͬһ�����εĸ��ʣ�
���𰸡���1��0.3
��2��75%��71
��3��![]()
��������
���ݸ����Ƶ��֮�͵���1�����ɵó��ɼ���![]() ��Ƶ�ʡ�
��Ƶ�ʡ�
�������⣬�����![]() ��
��![]() ��
��![]() ��
��![]() ���ĸ���Ƶ��֮�ͼ��ɹ��Ƴ����ο��Եļ����ʣ�����ÿ������ֵ�˸����Ƶ������� ���ɵó����ο��Ե�ƽ���֡�
���ĸ���Ƶ��֮�ͼ��ɹ��Ƴ����ο��Եļ����ʣ�����ÿ������ֵ�˸����Ƶ������� ���ɵó����ο��Ե�ƽ���֡�
�ɼ���![]() ������Ϊ4�ˣ��ɼ���
������Ϊ4�ˣ��ɼ���![]() ������Ϊ2�ˣ��ӳɼ���
������Ϊ2�ˣ��ӳɼ���![]() ��
��![]() ��ѧ����ѡ���ˣ���������
��ѧ����ѡ���ˣ���������![]() ��4�˱��Ϊ
��4�˱��Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �����ε�2�˱��Ϊ
�����ε�2�˱��Ϊ![]() ��
��![]() ��������ѡ���ˣ�������¼����ɼ���
��������ѡ���ˣ�������¼����ɼ���![]() ��15��������ͬһ�������ڵ��¼����������¼�Ϊ7�������ùŵ���ͼ��㹫ʽ���ɵó���
��15��������ͬһ�������ڵ��¼����������¼�Ϊ7�������ùŵ���ͼ��㹫ʽ���ɵó���
��1����Ϊ�����Ƶ��֮�͵���1�����Գɼ���![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]() ��
��
��ȫƵ�ʷֲ�ֱ��ͼ��ͼ��ʾ��

��2���������⣬60�ּ����ϵķ�����![]() ��
��![]() ��
��![]() ��
��![]() ���ĸ��飬��Ƶ��֮��Ϊ
���ĸ��飬��Ƶ��֮��Ϊ![]() ���ʱ��ο��Եļ�����Ϊ75%
���ʱ��ο��Եļ�����Ϊ75%
������ֵ����ѧ���ɼ���ƽ���֣�����
![]()
���Ա��ο��Ե�ƽ����Ϊ71�֡�
��3���ɼ���![]() ������Ϊ
������Ϊ![]() �ˣ��ɼ���
�ˣ��ɼ���![]() ������Ϊ
������Ϊ![]() ��
��
�ӳɼ���![]() ��
��![]() ��ѧ����ѡ���ˣ���������
��ѧ����ѡ���ˣ���������![]() ��4�˱��Ϊ
��4�˱��Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �����ε�2�˱��Ϊ
�����ε�2�˱��Ϊ![]() ��
��![]() ��������ѡ���ˣ�������¼����ɼ���
��������ѡ���ˣ�������¼����ɼ���
![]()
��15��������ͬһ�����������������¼�Ϊ��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
��7�����ʸ���![]()


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1����![]() ʱ������
ʱ������![]() �Ķ�����
�Ķ�����
��2��������![]() ���ҽ���һ����㣬��ʵ��m��ȡֵ��Χ��
���ҽ���һ����㣬��ʵ��m��ȡֵ��Χ��
��3����ȡ![]() ��������ʽ
��������ʽ![]() ������
������![]() ���������ʵ��m��ȡֵ��Χ��
���������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��ϱ���ʱ��������ѧ���敜������敜ԭ���������Ƽ�ͬ����������족.��˼�ǣ�������ƽ��ƽ�������������壬��ƽ����������ƽ��ƽ����κ�ƽ�����أ����صõ����������������ȣ����������������������.Ϊ����������������һ������뾶�߶�����뾶��ȵ�Բ����Ȼ����Բ������ȥһ����Բ���µ���Բ��Ϊ���㣬Բ���ϵ���Ϊ�����Բ�������敜ԭ����֤���˼���������������ȣ��κ�һ��ƽ�����ص����������������ȣ�.����Բ![]() ��
��![]() ����תһ�ܺ��һ���״�ļ����壬������������������敜ԭ���������������ڣ� ��
����תһ�ܺ��һ���״�ļ����壬������������������敜ԭ���������������ڣ� ��
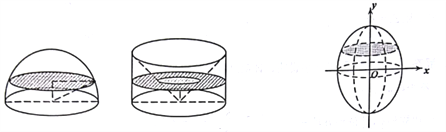
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABC��A1B1C1������ABB1A1Ϊ���Σ�����ACC1A1Ϊ�����Σ�����ABB1A1�Ͳ���ACC1A1��
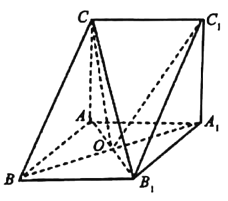
��1����֤��A1B��ƽ��AB1C��
��2����AB��2����ABB1��60����������C1��COB1�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ��
��![]() ʱ��������
ʱ��������![]() ��
��![]() ��ֵ��
��ֵ��
��2��������![]() �Ƕ�����
�Ƕ�����![]() �ϵ��溯��.
�ϵ��溯��.
�ٴ���![]() ��ʹ�ò���ʽ
��ʹ�ò���ʽ![]() �н⣬��ʵ��
�н⣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��������![]() ����
����![]() ����������
����������![]() ��
��![]() ������ʽ
������ʽ![]() ���������ʵ��
���������ʵ��![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������101��ѧУ����һ�����������������������һ�����ֽ��Һ�һ��ͼ��ݣ���ͼ���������ֽ�����A����ͼ�����B����Ϊ����A��B����֮��ľ��룬ijͬѧѡ������A��B�����ߵ�C�������ɡ�ABC�������Dz��������ݵIJ�ͬ�������ٲ�����A��AC��BC���ڲ�����A����B��BC���۲�����C��AC��BC���ܲ�����A����C����B. ����һ����Ψһȷ��A��B����֮��ľ�������з����������_______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=![]() ��ͼ���뺯��y=2sin��x����3��x��5����ͼ�����н���ĺ�����֮�͵��ڣ� ��
��ͼ���뺯��y=2sin��x����3��x��5����ͼ�����н���ĺ�����֮�͵��ڣ� ��
A��2 B��4 C��6 D��8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У� ��Բ
�У� ��Բ![]() ������������ԭ��
������������ԭ��![]() �����ҽ���Ϊ
�����ҽ���Ϊ![]() ���ҵ�
���ҵ�![]() ����Բ
����Բ![]() �ϣ�
�ϣ�

��1������Բ![]() �ķ��̣�
�ķ��̣�
��2������Բ�����Ҷ���ֱ�Ϊ![]() ��
��![]() ����Բ������
����Բ������![]() ������һ�㣬ֱ��
������һ�㣬ֱ��![]() ����Բ
����Բ![]() ����һ��
����һ��![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() ��
��![]() �㣬 ��֤��
�㣬 ��֤��![]() ������ͬһ��ֱ����
������ͬһ��ֱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �����������
�����������![]()
![]() ������
������![]() , ��
, ��![]() ʱ��
ʱ��![]() ����
����![]() .
.
( I ) ��![]() ��ֵ��
��ֵ��
(II) ��![]() ʱ������
ʱ������![]() �����ֵ����Сֵ��
�����ֵ����Сֵ��
(III) �躯��![]() ���жϺ���g(x)����м�����㣬�������ʱʵ��m��ȡֵ��Χ.
���жϺ���g(x)����м�����㣬�������ʱʵ��m��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com