
如图,四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
, 底面
底面

(1)证明: ;
;
(2)若 ,求二面角
,求二面角 余弦值.
余弦值.
科目:高中数学 来源:2013-2014学年陕西省等五校高三第二次联合模拟考试文科数学试卷(解析版) 题型:解答题
向量
 .函数
.函数 .
.
(1)若 ,求函数
,求函数 的单调减区间;
的单调减区间;
(2)将函数 的图像向左平移
的图像向左平移 个单位得到函数
个单位得到函数 ,如果函数
,如果函数 在
在 上至少存在2014个最值点,求
上至少存在2014个最值点,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省等五校高三第三次模拟文科数学试卷(解析版) 题型:选择题
下列命题正确的个数是 ( )
①命题“ ”的否定是“
”的否定是“ ”;
”;
②函数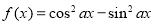 的最小正周期为
的最小正周期为 ”是“
”是“ ”的必要不充分条件;
”的必要不充分条件;
③ 在
在 上恒成立
上恒成立
 在
在 上恒成立;
上恒成立;
④“平面向量 与
与 的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“ ”.
”.
(A)1 (B)2 (C)3 (D)4
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省高考第七次适应性训练理科数学试卷(解析版) 题型:解答题
已知函数 .
.
(1)试判断函数 的单调性;
的单调性;
(2)设 ,求
,求 在
在 上的最大值;
上的最大值;
(3)试证明:对任意 ,不等式
,不等式 都成立(其中
都成立(其中 是自然对数的底数).
是自然对数的底数).
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省高考第七次适应性训练理科数学试卷(解析版) 题型:选择题
平面上有一组平行线且相邻平行线间的距离为 ,把一枚半径为
,把一枚半径为 的硬币任意平掷在这个平面,则硬币不与任何一条平行线相碰的概率是( )
的硬币任意平掷在这个平面,则硬币不与任何一条平行线相碰的概率是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省高考第七次适应性训练文科数学试卷(解析版) 题型:填空题
已知如下算法语句
输入t;
If t<5 Then y=t2+1;
Else if t<8 Then y=2t-1;
Else y= ;
;
End If
End if
输出y
若输入t=8,则下列程序执行后输出的结果是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省高三第六次模拟理科数学试卷(解析版) 题型:填空题
A.(坐标系与参数方程)已知直线的参数方程为 (为参数),圆
(为参数),圆 的参数方程为
的参数方程为 (
( 为参数), 则圆心
为参数), 则圆心 到直线的距离为_________.
到直线的距离为_________.
B.(几何证明选讲)如右图,直线 与圆
与圆 相切于点
相切于点 ,割线
,割线
 经过圆心
经过圆心 ,弦
,弦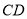 ⊥
⊥ 于点
于点 ,
,  ,
, ,则
,则 _________.
_________.
C.(不等式选讲)若存在实数 使
使 成立,则实数
成立,则实数
的取值范围是_________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com